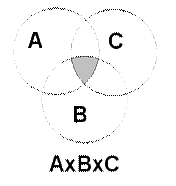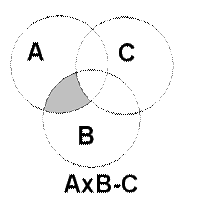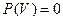Что понимается под случайным событием
Случайные события и их вероятности



1. Случайные события
Теория вероятностей— это раздел математики изучающий закономерности массовых случайных событий.
Случайным называется событие, наступление которого нельзя гарантировать. Случайность того или иного события определяется множеством причин, которые существуют объективно, но учесть их все, а также степень их влияния на изучаемое событие, невозможно. К таким случайным событиям относятся: выпадание того или иного числа при бросании игральной кости, выигрыш в лотереи, количество больных, записавшихся на прием к врачу и т.п.
И хотя в каждом конкретном случае трудно предсказать исход испытания, при достаточно большом числе наблюдений можно установить наличие некоторой закономерности. Подбрасывая монету, можно заметить, что число выпадания орла и решки примерно одинаково, а при бросании игральной кости различные грани также появляются, примерно одинаково. Это говорит о том, что случайным явлениям присущи свои закономерности, но они проявляются лишь при большом количестве испытаний. Правильность этого подтверждает закон больших чисел, который лежит в основе теории вероятностей.
Рассмотрим основные термины и понятия теории вероятностей.
Испытанием называется совокупность условий, при которых может произойти данное случайное событие.
События бывают достоверные, невозможные и случайные.
Достоверное событие — это событие, которое в результате испытания непременно должно произойти.
Например,если на игральной кости на всех шести гранях. нанести цифру 1, тогда выпадение цифры 1, при бросании кости, есть событие достоверное.
Например,в ранее рассмотренном примере — это выпадение любой цифры, кроме 1.
Случайное событие — это событие, которое при испытаниях может произойти или не произойти. Те или иные события реализуются с различной возможностью.
События называются несовместными, если в результате данного испытания появление одного из них исключает появление другого.
Например,при бросании монеты выпадение одновременно орла и решки есть события несовместные.
События называются совместными, если в результате данного испытания появление одного из них не исключает появление другого.
Например,при игре в карты появление валета и масти пик — события совместные.
События называются равновозможными, если нет оснований считать, что одно из них происходит чаше, чем другое!
Например,выпадение любой грани игрального кубика есть равновозможные события.
События образуют полную группу событий, если в результате испытания обязательно произойдет хотя бы одно из них и любые два из них несовместны.
Например,при 10 выстрелах в мишень возможно от 0 до 10 попаданий. При бросании игрального кубика может выпасть цифра от 1 до 6. Эти события образуют полную группу.
События, входящие в полную группу попарно несовместных и равновозможных событий, называются исходами, или элементарными событиями. Согласно определению достоверного события, можно считать, что событие, состоящее в появлении одного, неважно какого, из событий полной группы, есть событие достоверное.
Например,при бросании одного игрального кубика выпадает число меньше семи. Это пример достоверного события.
Частным случаем событий, образующих полную группу, являются противоположные события.
Два несовместных события А и 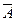
Например,если стипендия начисляется только при получении на экзамене хороших и отличных оценок, то события «стипендия» и «неудовлетворительная или удовлетворительная оценка» — противоположные.
Событие А называется благоприятствующим событию В, если появление события А влечет за собой появление события В.
Например,при бросании игрального кубика появлению нечетного числа благоприятствуют события, связанные с выпадением чисел 1,3 и 5.
2. Операции над событиями
Операции над событиями аналогичны операциям над множествами.
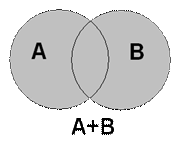
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.
Сумма событий может быть обозначена знаками «+», «È», «или».
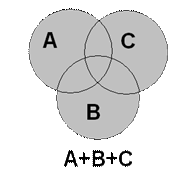
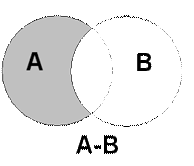
На рисунке 1 представлена геометрическая интерпретация с помощью диаграмм Эйлера-Венна. Сумме событий А + В будет соответствовать вся заштрихованная область.

Область пересечения событий А и В соответствует совместным событиям, которые могут произойти одновременно. Аналогично для событий А, В и С имеются совместные события А и В; А и С; В и С; А и В и С, которые могут про изойти одновременно.
Например,в урне находятся белые, красные и синие шары. Возможны следующие события: А — вынут белый шар; В — вынут красный шар; С — вынут синий шар. Событие В + С означает, что произошло событие — вынут цветной шар или вынут не белый шар.
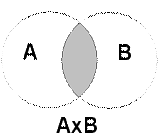
Произведением нескольких событий называется событие которое состоит в совместном наступлении всех этих событий в результате испытания.
Произведение событий может быть обозначено знаками «х», «∩», «и».
Геометрическая интерпретация произведения событий представлена на рис. 2.
Разностью двух событий А-В называется событие, состоящее из исходов, входящих в А, но не входящих в В.
На рис. 3 представлена иллюстрация разности событий с помощью диаграмм Эйлера-Венна.
Разностью двух событий А-В является заштрихованная область А без той части, которая входит в событие В. Разность между произведением событий А и В и событием С будет совместная площадь события А и события В без совместной с нею площадью события С.
3. Определение вероятности события
Классическое определение вероятности заключается в следующем. Если известны все возможные исходы испытания и нет оснований считать, что одно случайное событие появлялось бы чаще других, т.е. события равновозможны и несовместны, то имеется возможность аналитического определения вероятности события.
Вероятностью Р(А)события Аназывается отношение числа благоприятствующих исходов т к общему числу равновозможных несовместных исходов п:
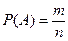
Свойства вероятности:
1. Вероятность случайного события А находится между 0 и 1.
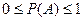
2. Вероятность достоверного события равна 1.
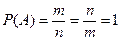
3. Вероятность невозможного события равна 0.
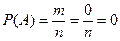
Случайное событие
Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.
Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом 

Содержание
Определение
Математически случайное событие — подмножество пространства элементарных исходов случайного эксперимента; элемент алгебры или сигма-алгебры событий 



Пример
Случайный эксперимент состоит в бросании игральной кости: пример случайного события — выпавшее число чётно; события «Выпала единица», «Выпала двойка» и т. д. — элементарные исходы эксперимента; совокупность всех событий «Выпала 1»..«Выпала 6» — полная группа событий.
См. также
Ссылки
Полезное
Смотреть что такое «Случайное событие» в других словарях:
случайное событие — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] случайное событие Событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная… … Справочник технического переводчика
Случайное событие — [random event, chance event] — событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная вероятность его наступления. То же (в разных источниках) исход, случай, результат… … Экономико-математический словарь
СЛУЧАЙНОЕ СОБЫТИЕ — (в теории вероятностей) событие, которое может при осуществлении данных условий (т. е. при данном испытании) как произойти, так и не произойти и для которого имеется определенная вероятность его наступления. Наличие у случайного события… … Большой Энциклопедический словарь
случайное событие — (в теории вероятностей), событие, которое может при осуществлении данных условий (то есть при данном испытании) как произойти, так и не произойти и для которого имеется определенная вероятность его наступления. Наличие у случайного события… … Энциклопедический словарь
случайное событие — atsitiktinis įvykis statusas T sritis fizika atitikmenys: angl. accidental event; chance event; random event vok. zufälliges Ereignis, n rus. случайное событие, n pranc. événement aléatoire, m … Fizikos terminų žodynas
Случайное событие — в теории вероятностей, событие, которое может при данных условиях как произойти так и не произойти и для которого имеется определённая Вероятность р (0 ≤ p ≤ 1) его наступления при данных условиях. Наличие у С. с. А определённой… … Большая советская энциклопедия
СЛУЧАЙНОЕ СОБЫТИЕ — любая комбинация исходов нек рого опыта, имеющая определенную вероятность наступления. Пример 1. При бросании двух игральных костей каждый из 36 исходов опыта может быть представлен нарой (i, j), где i число очков на верхней грани цервой кости, а … Математическая энциклопедия
СЛУЧАЙНОЕ СОБЫТИЕ — (в теории вероятностей), событие, к рое может при осуществлении данных условий (т. е. при данном испытании) как произойти, так и не произойти и для к рого имеется определ. вероятность его наступления. Наличие у С. с. определ. вероятности р… … Естествознание. Энциклопедический словарь
Случайное событие — (в теории вероятностей) событие, которое может, с определенной долей вероятности, в условиях испытания как произойти, так и не произойти; отдельный исход (результат) испытания. См. Случайная величина. Случайный процесс … Начала современного естествознания
событие — Факт, состоящий в том, что нечто произошло или в проблемной области, или в среде, или в информационной системе. [ГОСТ 34.320 96] событие 1. См. Случайное событие. 2. В сетевом планировании и управлении — промежуточный или окончательный… … Справочник технического переводчика
ПОНЯТИЕ СЛУЧАЙНОГО СОБЫТИЯ



ОСНОВНЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.
Второе дыхание – Задачник 1
Случайное событие это всякий факт, который в результате опыта может произойти или не произойти при выполнении определенного комплекса условий (КУ).
           |
Испытанием называется многократное проведение опыта.
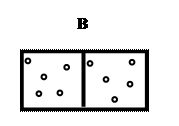
В теории вероятностей события бывают совместимые и несовместимые.
Несовместимые события, т.е. взаимоисключающие события.
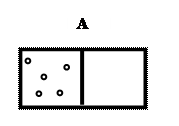  |
Противоположные события являются частным случаем несовместимых событий.
Достоверные и невозможные события.
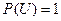
Смена дня и ночи на нашей широте.
Полной группой событий будем называть такие случайные события, которые попарно несовместимы и для которых при каждом испытании обязательно произойдет хотя бы одно из них.
Что понимается под случайным событием
Событиями являются и результаты различных опытов, наблюдений и измерений.
1) из ящика с разноцветными шарами наугад вытаскивают белый шар;
2) на один из приобретенных лотерейных билетов выпал выигрыш;
3) при бросании игральной кости выпала цифра 6.
События делятся на достоверные, случайные и невозможные.
Достоверным называется событие, если оно обязательно произойдет в данном испытании.
Случайным называется событие, если оно может произойти, но может и не произойти в данном испытании.
Невозможным называется событие, если оно не может произойти в данном испытании.
За единицу принимают вероятность достоверного события, а вероятность невозможного события считают равной нулю. Тогда вероятность Р любого события А удовлетворяет неравенству:
Несовместными называются события, если появление одного из них
Пример. Опыт состоит в подбрасывании монеты, событие А – выпадение орла, событие В – выпадение решки. Эти события несовместны, равновозможны и единственно возможны.
Равновозможными называются события, если ни одно из них не является более возможным, чем другое.
Единственно возможными называются события, если в результате опыта хотя бы одно из них обязательно наступит. Говорят, что единственно возможные события образуют полную группу событий .
Рассмотрим классический метод определения вероятности некоторого случайного события. Пусть в результате некоторого опыта могут наступить события А1, А2, А3, …, Аn (элементарные исходы опыта), которые являются:
1)единственно возможными, т.е. в результате опыта хотя бы одно из них обязательно наступит;
2)несовместными, т.е. появление одного из них исключает появление всех остальных;
3)равновозможными, т.е. не существует никаких причин, в связи с которыми одно из событий появлялось бы чаще, чем остальные.
Пусть при появлении некоторых из этих событий наступает событие А. Обозначим число таких событий k (k≤n). А при появлении остальных (n-k) событий событие А не наступает. Говорят, что k событий (элементарных исходов), при которых появляется событие А, благоприятствуют событию А, а остальные (n-k) событий не благоприятствуют ему.
Вероятностью события А называется отношение числа k элементарных исходов, благоприятствующих этому событию, к общему числу элементарных исходов испытания n, если они равновозможны, несовместны и единственно возможны.
Случайные события. Вероятность случайного события
Если событие при рассматриваемых условиях происходит всегда, то оно называется достоверным. Вероятность появления достоверного события равна 1. Так, например, событие «Лето составляет 92 дня» является достоверным.
Если событие при рассматриваемых условиях не происходит никогда, то оно называется невозможным. Вероятность появления невозможного события равна 0. Так, например, событие «После декабря наступит май» является невозможным.
Вероятность случайного события может быть любым числом от 0 до 1.
Определение вероятности:
Если эксперимент заканчивается одним из 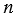 равновероятных исходов, из которых равновероятных исходов, из которых 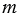 являются благоприятными для наступления данного события, то вероятность этого события равна являются благоприятными для наступления данного события, то вероятность этого события равна 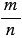 . . |
Вероятность события обозначается буквой 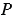
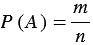
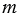
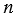
Пример: Какова вероятность того, что при бросании игрального кубика выпадет: 1) менее трех очков; 2) более шести очков; 3) не более шести очков.
Решение:
1) При бросании кубика может произойти 6 равновероятных исходов: выпадет 1, 2, 3, 4, 5 или 6 очков. Из них благоприятными являются два исхода: выпадет 1 очко или выпадет 2 очка, т.к. 1 меньше 3 и 2 меньше 3. Поэтому искомая вероятность 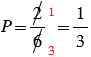
2) При бросании кубика может произойти 6 равновероятных исходов: выпадет 1, 2, 3, 4, 5 или 6 очков. Из них нет ни одного благоприятного исхода, т.к. более шести очков на кубике выпасть не может, значит, рассматриваемое событие является невозможным и его вероятность 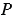
3) При бросании кубика может произойти 6 равновероятных исходов: выпадет 1, 2, 3, 4, 5 или 6 очков. Из них все исходы являются благоприятными, т.к. любое из чисел 1, 2, 3, 4, 5, 7 меньше 7, значит, рассматриваемое событие является достоверным и его вероятность 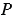
Ответ: 1) 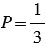
Поделись с друзьями в социальных сетях: