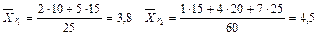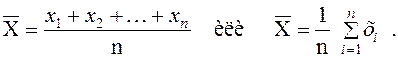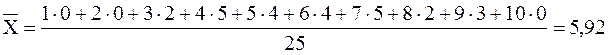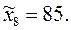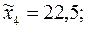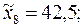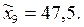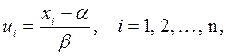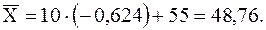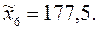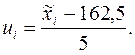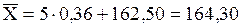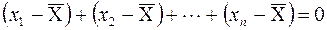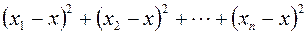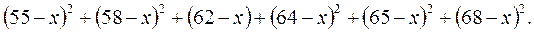Что понимается под выборочной средней

Выборочная средняя и выборочная дисперсия

Пусть для изучения генеральной совокупности относительно количественного признака Х произведена выборка объёма n.

Выборочной средней называется среднее арифметическое значение выборки.

Если все значения х₁, х₂, …, х_n выборки различны, то

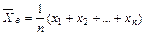(7.1)

(7.2)

Иногда бывает целесообразным выборочные значения случайной величины разбить на отдельные группы. Для каждой группы можно найти её среднюю.

Групповой средней называется среднее арифметическое значений выборки, принадлежащих группе.

По групповым средним можно найти среднее для всей выборки.

Общей средней называется среднее арифметическое значение групповых средних.

Пример 7.1.Найти общую среднюю на основе выборки.

Решение: Находим групповые средние:

Если варианты х_i – большие числа, то для облегчения вычисления выборочной средней используют следующий приём. Пусть С – константа.

, то формула (7.1) преобразуется к виду:

(7.3)

Пример 7.2.Имеется выборка:

Найти выборочную среднюю.

Решение: Берем С=72 и вычисляем разности

Их сумма: α₁+α₂+…+α₁₀=-0,38; их среднее арифметическое: ; выборочная средняя: .

Для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки относительно выборочного среднего вводят понятие выборочной дисперсии.

Выборочной дисперсией D_в называется среднее арифметическое квадратов отклонений наблюдаемых значений признака Х от выборочной средней .

Если все значения х₁, х₂, …, х_n признака выборки объёма n различны, то

(7.4)

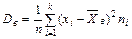(7.5)

Пример 7.3.Выборочная совокупность задана таблицей распределения:

Найти выборочную дисперсию.

Решение: Согласно формулам (7.2) и (7.5) имеем:

.

Выборочным средним квадратическим отклонением называется квадратный корень из выборочной дисперсии:

Можно доказать, что

(7.6)

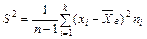(7.7)

Исправленная дисперсия (7.7) является несмещенной оценкой генеральной дисперсии

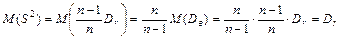Если варианты х_i – большие числа, то для облегчения вычисления выборочной дисперсии D_в формулу (7.4) преобразуют к следующему виду:

(7.8)

где С – ложный нуль.

Пример 7.4.Через каждый час измерялось напряжение тока в электросети. Результаты измерений в вольтах представлены в таблице 7.1:

Найти оценки для математического ожидания и дисперсии результатов измерений.

Решение: Оценки для математического ожидания и дисперсии найдем по формулам (7.3) и (7.8), положив С=220. Все необходимые вычисления приведены в таблице 7.2:

Источник

Выборочное среднее

Теперь рассмотрим наиболее часто используемое понятие среднего, которое в отличие от моды и медианы объединяет все выборочные значения.

Определение 2.3Средним арифметическим выборки x₁, x₂, …, x_n значений случайной величины Х называется число , равное сумме всех выборочных значений, деленной на число всех наблюдений n:

Обычно среднее арифметическое 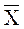называется выборочным средним или простосредним.

В случае, когда выборка совпадает со всей исследуемой генеральной совокупностью, то таким же образом вычисляется её генеральное среднее. В дальнейшем выборочное среднее всей генеральной совокупности значений случайной величины Х будем обозначать символами или и называть генеральным средним.

Пример 2.7 Студент Денисов по пяти предметам получил следующие экзаменационные оценки по десятибальной системе: 8, 9, 8, 7, 6. Вычислим среднее данных оценок:

.

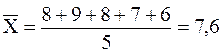
Подчеркнем, что выборочное среднее не обязательно должно быть элементом самой выборки. В том случае, когда выборка представляется вариационным рядом, содержащим вариант x₁, x₂, …, x_k с соответствующими частотами , то среднее вычисляется по следующей формуле:

,

, где .

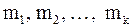
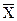
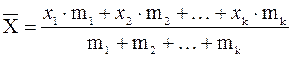
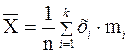
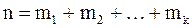
Пример 2.8 Результаты экзамена по математике для группы студентов, состоящей из 25 человек, представлены следующим вариационным рядом:

Таблица 2.7 –Экзаменационные оценки группы студентов

Оценки

Пример 2.9Для вариационного ряда данных о посещаемости университетской библиотеки из примера 1.6., найдем среднее, моду и медиану:

Таблица 2.8 –Вариационный ряд данных посещаемости библиотеки

Число посещений	0 1 2 3 4 5
	5 6 7 2 3 2

.

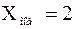
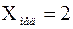
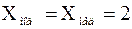
Очевидно, что мода данного ряда . Легко находится и медиана . Среднее меньше моды и медианы, равным 2. Равенство приводит к предположению о симметричности этого распределения.

В случае, когда выборка сгруппирована в виде статистического ряда, состоящего из k интервалов

, , …, , …, ,

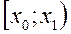
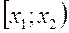
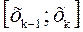
то конкретные выборочные значения могут быть неизвестными, и рассмотренные выше формулы не пригодны для вычисления среднего. Поэтому для каждого интервала вычисляется его середина, или интервальное среднее по формуле:

.

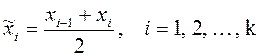
При выполнении вычислений каждое выборочное значение, принадлежащее интервалу, заменяется интервальным средним.

Определение 2.4Если – интервальные средние, а – соответствующие частоты всех интервалов статистического ряда, то выборочное среднее определяется формулой:

,

.

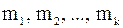
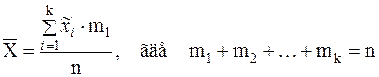
Пример 2.10 Найдем выборочное среднее возраста пациентов поликлиники по данным статистического ряда из примера 1.3.

Таблица 2.9 – Данные исследования возраста пациентов поликлиники

Возраст	10–20	20–30	30–40	40–50	50–60	60–70	70–80	80–90

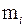Вычислим интервальные средние всех интервалов:

Найдем выборочное среднее:

Среднее характеризует средний возраст наиболее нуждающихся в лечении пациентов.

Пример 2.11 Найдем выборочное среднее для статистического ряда из примера 1.8. по данным о высоте зданий:

Таблица 2.10 –Данные исследования высоты зданий

Высота зданий	5–10 7,5	10–15 12,5	15–20 17,5	20–25 22,5	25–30 27,5	30–35 32,5	35–40 35,4	40–45 42,5	45–50 47,5

Объем исследуемой выборки . Вычислим интервальные средние:

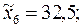
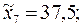
Найдем выборочное среднее:

Итак, метров – это среднее высот зданий данной выборки.

Существуют различные приемы, облегчающие вычислительную работу при нахождении выборочного среднего.

Если выборка содержит большие числа или многократно повторяющиеся близкие значения, то статистические данные можно преобразовать с помощью следующего равенства:

где и – любые действительные числа, причем .

Число подбирается так, чтобы разности были бы наименьшими, число изменяет масштаб данных.

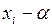
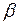
В результате преобразования данная выборка x₁, x₂, …, x_n заменяется выборкой 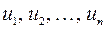с такими же соответствующими частотами.

Выборочная средняя выражается через выборочную среднюю по формуле:

.

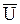
Правильный подбор значений и обычно облегчает нахождение среднего.

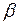
Отметим, что при вычислении выборочных числовых показателей удобно пользоваться определенными расчетными таблицами, в которые обычно записывают необходимые промежуточные результаты.

Пример 2.12Найдем среднее возраста пациентов поликлиники по статистическому ряду из примера 1.3., используя преобразования выборочных данных.

Таблица 2.11 –Данные исследования возраста пациентов поликлиники

Возраст	10–20	20–30	30–40	40–50	50–60	60–70	70–80	80–90

Положим, что . Такой выбор обусловлен тем, что именно это значение имеет наибольшую частоту. В качестве выберем длину интервалов, то есть .

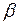
Запишем формулу преобразования выборки:

Все необходимые расчеты будем записывать в следующей таблице.

Таблица 2.12 –Вычисления среднего возраста пациентов поликлиники

Найдем .

Выборочное среднее вычислим по следующей формуле:

Это значение 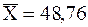совпадает с ранее найденным значением из примера 2.10.

Пример 2.13 Следующий статистический ряд представляет результаты проведенного измерения роста пятидесяти семнадцатилетних девушек.

Таблица 2.13 –Данные измерения роста

Рост Х	150–155 152,5	155–160 157,5	160–165 162,5	165–170 167,5	170–175 172,5	175–180 177,5
Частота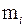

Для вычисления среднего, прежде всего найдем интервальные средние:

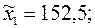
В качестве выберем интервальное среднее с наибольшей частотой: . Положим , что совпадает с длиной интервалов.

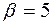
Преобразуем данные по формуле:

Дальнейшие вычисления записываем в следующей таблице:

Таблица 2.14 –Вычисление среднего роста девушек

Получаем

Найдем выборочное среднее по формуле:

Таким образом, выборочное среднее данной выборки равно 164,3.

Заметим, что выборочное среднее несгруппированной выборки в общем виде отличается от выборочного среднего этой выборки, вычисленного после группировки. Однако, для большинства исследований это различие является несущественным.

Формулу для вычисления среднего вариационного ряда можно преобразовать следующим образом:

,

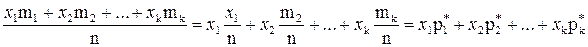
где , , …, – относительные частоты соответствующих значений. Известно что, при неограниченном увеличении числа испытаний относительная частота стремится к вероятности события:

, , …,

.

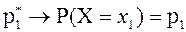
Отсюда следует, что

.

Таким образом, при увеличении числа испытаний среднее стремится к математическому ожиданию MX случайной величины Х, поэтому выборочное среднее является статистическим аналогом математического ожидания и обладает основными свойствами математического ожидания. Главное же отличие состоит в том, что математическое ожидание исследуемой случайной величины является постоянной величиной, а среднее является случайной величиной, так как его значение определяется случайной выборкой. Разные выборки из одной и той же генеральной совокупности могут иметь разные средние.

Определение 2.5 Число 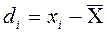называется отклонением выборочного значения x_i от среднего .

Пример 2.14 Администратор учреждения зафиксировал реальное время, затраченное на обеденный перерыв шестью сотрудниками: 55, 58, 62, 64, 65, 68.

.

Найдем отклонения от среднего:

Теперь найдем сумму всех отклонений:

.

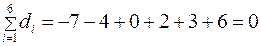
В данном примере сумма всех отклонений от среднего равна 0. Такой результат справедлив и в самом общем случае.

Теорема 2.1 Сумма всех отклонений выборочных значений x₁, x₂, …, x_n от их среднего равна 0.

Это свойство среднего подтверждает его центральную роль в совокупности выборочных данных. Равенство

показывает, что выборочные значения окружают среднее как справа, так и слева.

Интересное свойство среднего связано с суммой квадратов отклонений выборочных значений:

Теорема 2.2 Если x₁, x₂, …, x_n – случайная выборка со средним , то сумма квадратов разностей

принимает свое минимальное значение при .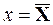

Например, запишем сумму квадратов разностей для выборки 55, 58, 62, 64, 65, 68 из предыдущего примера:

Ранее мы нашли среднее данной выборки Из тео-ремы 2.2 следует, что эта сумма имеет минимальное значение при .

Выборочная средняя находит более широкое применение, чем другие средние, в практических и теоретических исследованиях. Среднее арифметическое обобщает все значения исследуемой выборки и часто используется в качестве единого представителя всей совокупности выборочных данных. Например, при многократных экспериментальных измерениях некоторой величины за истинное значение часто принимается выборочное среднее. Тем не менее, между средним и каждым индивидуальным выборочным значением существует определенное различие.

Дата добавления: 2015-09-10 ; просмотров: 33 | Нарушение авторских прав

Источник