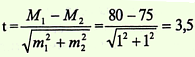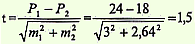Что понимают под достоверностью статистических показателей
Понятие о статистической достоверности
Статистическая достоверность имеет существенное значение в расчетной практике ФКС. Ранее было отмечено, что из одной и той же генеральной совокупности может быть избрано множество выборок:
— если они подобраны корректно, то их средние показатели и показатели генеральной совокупности незначительно отличаются друг от друга величиной ошибки репрезентативности с учетом принятой надежности;
— если они избираются из разных генеральных совокупностей, различие между ними оказывается существенным. В статистике повсеместно рассматривается сравнение выборок;
— если они отличаются несущественно, непринципиально, незначительно, т. е. фактически принадлежат одной и той же генеральной совокупности, различие между ними называется статистически недостоверным.
Статистически достоверным различием выборок называется выборка, которая различается значимо и принципиально, т. е. принадлежит разным генеральным совокупностям.
В ФКС оценка статистической достоверности различий выборок означает решение множества практических задач. Например, введение новых методик обучения, программ, комплексов упражнений, тестов, контрольных упражнений связано с их экспериментальной проверкой, которая должна показать, что испытуемая группа принципиально отлична от контрольной. Поэтому применяют специальные статистические методы, называемые критериями статистической достоверности, позволяющие обнаружить наличие или отсутствие статистически достоверного различия между выборками.
Все критерии делятся на две группы: параметрические и непараметрические. Параметрические критерии предусматривают обязательное наличие нормального закона распределения, т.е. имеется в виду обязательное определение основных показателей нормального закона — средней арифметической величины х и среднего квадратического отклонения о. Параметрические критерии являются наиболее точными и корректными. Непараметрические критерии основаны на ранговых (порядковых) отличиях между элементами выборок.
Приведем основные критерии статистической достоверности, используемые в практике ФКС: критерий Стьюдента, критерий Фишера, критерий Вилкоксона, критерий Уайта, критерий Ван-дер-Вардена (критерий знаков).
Критерий Стьюдента назван в честь английского ученого К. Госсета (Стьюдент — псевдоним), открывшего данный метод. Критерий Стьюдента является параметрическим, используется для сравнения абсолютных показателей выборок. Выборки могут быть различными по объему.
Критерий Стьюдента определяется так.
1. Находим критерий Стьюдента t по следующей формуле:
где Xi, x2 — средние арифметические сравниваемых выборок; /яь w2 — ошибки репрезентативности, выявленные на основании показателей сравниваемых выборок.
2. Практика в ФКС показала, что для спортивной работы достаточно принять надежность счета Р = 0,95.
3. На основании свойств нормального закона распределения в критерии Стьюдента осуществляется сравнение t и t^.
— если t > ftp, то различие между сравниваемыми выборками статистически достоверно;
Дата добавления: 2015-06-17 ; просмотров: 4093 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Раздел 6. Статистическая оценка достоверности результатов исследования



Под достоверностью статистических показателей следует понимать степень их соответствия отображаемой ими действительности. Достоверными результатами считаются те, которые не искажают и правильно отражают объективную реальность.
Оценить достоверность результатов исследования означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность.
В большинстве медицинских исследований врачу приходится, как правило, иметь дело с частью изучаемого явления, а выводы по результатам такого исследования переносить на все явление в целом — на генеральную совокупность.
Таким образом, оценка достоверности необходима для того, чтобы по части явления можно было бы судить о явлении в целом, о его закономерностях.
| Мера достоверности результатов (ошибка репрезентативности) | |||
При среднеарифметической (M) 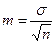 | При относительной величине (P) 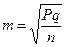 | ||
| Практическое применение Позволяет определить вероятность с которой возможно перенести результаты изучения с выборочной совокупности на генеральную совокупность | |||
| Способы оценки достоверности | |||
| Доверительные границы параметра | Достоверность разницы параметра | ||
| (При М) M±tm | (При P) P±tm | При средних арифметических 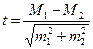 | При относительных величинах 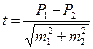 |
| Доверительная вероятность в медицинских исследованиях | |||
| В медико-биологических исследованиях вероятность 95% и более, т.е. при минимуме удвоенной ошибки (t=2) | Разница достоверна при t≥2 с вероятностью 95% и более |
Оценка достоверности результатов исследования предусматривает определение:
1) ошибок репрезентативности (средних ошибок средних арифметических и относительных величин) — m
2) доверительных границ средних (или относительных) величин
3) достоверности разности средних (или относительных) величин (по критерию t)
4) достоверности различия сравниваемых групп по критерию χ 2
Оценка достоверности результатов статистического исследования
Под достоверностью статистических показателей следует понимать степень их соответствия отображаемой ими действительности.
Оценить достоверность результатов исследования означает определить, с какой вероятностью безошибочного прогноза возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность.
Оценка достоверности результатов исследования предусматривает определение:
1) ошибок репрезентативности – m
2) доверительных границ средних (или относительных ) величин;
3) достоверности разности средних (или относительных) величин (по критерию t)
4) достоверности различия сравниваемых групп по критерию x 2
По размерам средней ошибки можно судить, насколько найденная выборочная средняя величина отличается от средней генеральной совокупности. Утроенная средняя ошибка не должна превышать самого показателя, т.е. средней или относительной величины.
На величину средней ошибки средней арифметической влияют следующие два обстоятельства. Во-первых, однородность собранного материала: чем меньше разбросанность вариант вокруг своей средней, тем меньше ошибка репрезентативности. Во-вторых, число наблюдений: средняя ошибка будет тем меньше, чем больше число наблюдений.
Доверительные границы – границы средних и относительных величин, выход за пределы которых вследствие случайных колебаний имеет не значительную вероятность.
Достоверность разности между двумя сравниваемыми величинами применяется, когда необходимо оценить достоверность различия средних или относительных показателей двух групп.
Полученный критерий t оценивается по общепринятым правилам:
При числе единиц наблюдения более 30, если t больше или равно 2, различие показателей следует считать достоверным, т.е. оно соответствует вероятности безошибочного прогноза, равной 95% (0,95), а вероятность ошибки – 5% (0,05).
При числе наблюдений меньше 30, для оценки вероятности безошибочного прогноза используют таблицу стандартных значений Стьюдента.
3.1. Контрольные задания по теме: оценка достоверности разности средних и относительных величин
Среднее число дней временной нетрудоспособности больных гипертонической болезнью
| Контингент больных | Число дней нетрудоспо-собности (М) | m | t | p |
| До санаторного лечения После санатор-ного лечения | 9,82 5,89 | ±0,67 ±0,60 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Частота госпитализации рабочих химического предприятия
| Число госпитализации (в %) | m | t | p |
| Мужчины Женщины | 113,1 101,8 | ±12,0 ±9,4 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
ЗАДАЧА №3
Распространенность ревматизма среди детей дошкольного возраста
| Распространенность (в %) | m | t | p |
| Мальчики Девочки | 6,2 9,3 | ±0,5 ±0,6 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Частота абортов при первой беременности среди женщин с различным семейным положением
| Семейное положение | Частота абортов (в %) (р) | m | t | p |
| Незарегистрированный брак Одинокие | 50 73 | ±4,0 ±3,0 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
ЗАДАЧА№ 5
Послеоперационная летальность больных раком шейки матки при различных методах лечения
| Оперирован-ные | Летальность (в %) (Р) | m | t | p |
| Без предварительного облучения После предварительного облучения | 6,0 2,1 | ±1,5 ±0,7 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Распространенность ревматизма среди школьников
| Распространенность ревматизма (в %) | m | t | p |
| Мальчики Девочки | 1,9 2,7 | ±0,2 ±0,2 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Частота диагностических ошибок, допускаемых врачами с различным стажем работы
| Стаж | Частота ошибочных диагнозов (в %) | m | t | p |
| До 5 лет Свыше 5 лет | 15,3 6.1 | ±2,9 ±1.6 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Частота случаев временной нетрудоспособности среди женщин, имеющих детей, и бездетных
| Число случаев нетрудоспособности на 100 женщин (р) | m | t | p |
| Имеющие детей Бездетные | 166 107 | ±19,0 ±20,0 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Восстановление трудоспособности у больных, перенесших инфаркт миокарда
| Число лиц, возвратившихся к труду в % (Р) | M | t | P |
| Инфаркт миокарда без гипертонической болезни Инфаркт миокарда с гипертонической болезнью | 75 61 | ±3,0 ±4,0 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
ЗАДАЧА № 10
Частота абортов при первой беременности среди женщин с различным семейным положением
| Семейное положение | Частота абортов в % | M | t | р |
| Зарегистрированный брак Одинокие | 12 73 | ±2,0 ±3,0 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Частота абортов среди работающих женщин, имеющих различные жилищно-бытовые условия
| Число госпитализации (в %) | M | t | p |
| Хорошие и удовлетворительные Неудовлетворительные | 9 12 | ±1,0 ±0,9 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Успеваемость студентов медицинского института неработающих и совмещающих учебу с работой.
| Студенты | Средний балл М | M | t | p |
| Неработающие Совмещающие учебу с работой | 4,1 3,85 | ±0,09 ±0,05 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Успеваемость мужчин и женщин, студентов медицинского института.
| Студенты | Средний балл М | M | t | p |
| Женщины Мужчины | 4,03 3,86 | ±0,04 ±0,04 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Заболеваемость мужчин и женщин старше 50 лет
| Заболеваемость (‰) | M (‰) | t | P |
| Мужчины Женщины | 1507 1426 | ±12 ±8 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Младенческая смертность в городской и сельской местности Мордовии за 2002 г.
| Младенческая смертность (‰) | M | t | p |
| Городская местность Сельская местность | 9,00 8,60 | ±0,13 ±0,15 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Летальность в городских больницах
| Больницы | Летальность (%) (Р) | m(%) | t | p |
| А Б | 2,70 3,20 | ±0,07 ±0,04 |
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод
Определить достоверность различий сравниваемых групп и сделать соответствующий вывод.
Проект Extra.im
В практической и научно-практической работе врачи обобщают результаты, полученные как правило на выборочных совокупностях. Для более широкого распространения и применения полученных при изучении репрезентативной выборочной совокупности данных и выводов надо уметь по части явления судить о явлении и его закономерностях в целом.
Учитывая, что врачи, как правило, проводят исследования на выборочных совокупностях, теория статистики позволяет с помощью математического аппарата (формул) переносить данные с выборочного исследования на генеральную совокупность. При этом врач должен уметь не только воспользоваться математической формулой, но сделать вывод, соответствующий каждому способу оценки достоверности полученных данных. С этой целью врач должен знать способы оценки достоверности. Применяя метод оценки достоверности результатов исследования для изучения общественного здоровья и деятельности учреждений здравоохранения, а также в своей научной деятельности, исследователь должен уметь правильно выбрать способ данного метода. Среди методов оценки достоверности различают параметрические и непараметрические.
Параметрическими называют количественные методы статистической обработки данных, применение которых требует обязательного знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.
Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.
Как параметрические, так и непараметрические методы, используемые для сравнения результатов исследований, т.е. для сравнения выборочных совокупностей, заключаются в применении определенных формул и расчете определенных показателей в соответствии с предписанными алгоритмами. В конечном результате высчитывается определенная числовая величина, которую сравнивают с табличными пороговыми значениями. Критерием достоверности будет результат сравнения полученной величины и табличного значения при данном числе наблюдений (или степеней свободы) и при заданном уровне безошибочного прогноза.
Таким образом, в статистической процедуре оценки основное значение имеет полученный критерий достоверности, поэтому сам способ оценки достоверности в целом иногда называют тем или иным критерием по фамилии автора, предложившего его в качестве основы метода.
| Применение параметрических методов |
При проведении выборочных исследований полученный результат не обязательно совпадает с результатом, который мог бы быть получен при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную совокупность.
| Средняя ошибка средней арифметической величины определяется по формуле: | 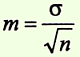 | где σ — среднеквадратическое отклонение n — число наблюдений |
| Ошибка относительного показателя определяется по формуле: | 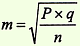 | где p — показатель, выраженный в %, ‰, %оо и т.д. q = (100 — р), при p выраженном в %; или (1000 — р), при p выраженном в ‰ или (10000 — р), при p выраженном в %оо и т.д. |
| При числе наблюдений меньше 30 ошибки репрезентативности определяются соответственно по формулам: | 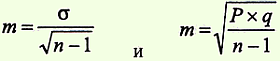 | |
| Определение доверительных границ средних и относительных величин |
Формулы определения доверительных границ представлены следующим образом:
Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности.
Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности.
При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза (Р).
Для большинства медико-биологических исследований считается достаточной степень вероятности безошибочного прогноза, равная 95%, а число случаев генеральной совокупности, в котором могут наблюдаться отклонения от закономерностей, установленных при выборочном исследовании, не будут превышать 5%. При ряде исследований, связанных, например, с применением высокотоксичных веществ, вакцин, оперативного лечения и т.п., в результате чего возможны тяжелые заболевания, осложнения, летальные исходы, применяется степень вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной совокупности возможны отклонения от закономерностей, установленных в выборочной совокупности.
Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений.
При n>30 степени вероятности безошибочного прогноза Р = 99,7% — соответствует значение t = 3, а при Р = 95,5% — значение t = 2.
При п
| Оценка достоверности разности результатов исследования |
Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены какой-то причиной, различия между двумя средними величинами или относительными показателями.
Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие причинно-следственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них.
Формулы определения достоверности разности представлены следующим образом:
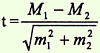 для средних величин | 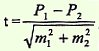 для относительных показателей | где t — критерий достоверности, m1 и m2 — ошибки репрезентативности, М1 и М2 — средние величины, Р1 и Р2 — относительные показатели. |
Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности.
При t
Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
| Задача — эталон |
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24% (m = ± 2,64%).
Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.
Решение.
Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов
Оценка достоверности результатов статистического исследования (относительные величины).
При изучении генеральной (сплошной) совокупности для ее количественной характеристики достаточно расчитать Mи σ. Однако на практике, как правило, исследование проводят на выборочной совокупности, которая должна быть репрезентативно (достоверна) или представительна для генеральной совокупности. Репрезентативность выборочной совокупности оценивают специальными методами отбора, она означает представительность в ней всех учитываемых признаков генеральной совокупности.
Под достоверностью статистических показателей следует понимать степень их соответствия отображаемой ими действительности. Достоверными результатами считаются те, которые не искажают и правильно отражают объективную реальность.
Оценить достоверность результатов исследования означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность.
В большинстве медицинских исследований врачу приходится, как правило, иметь дело с частью изучаемого явления, а выводы по результатам такого исследования переносить на все явление в целом – на генеральную совокупность.
Таким образом оценка достоверности необходима для того, чтобы по части явления должно было бы судить о явлений в целом, о его закономерности.
Оценка достоверности результатов исследования предусматривает вычмсление:
1) Ошибок репрезентативности (средней ошибки m для средних M или относительных P величин;
2) Доверительных границ средних (M) или относительных (P) величин;
3) Достоверности разности средних (M) или относительных (P) величин по критерию t.
4) Достоверности различия сравниваемых групп по критерию X 2 (хи-квадрат).
2.2. Определение средней ошибки средней (или относительной) величины (ошибки репрезентативности) – m.
Ошибка репрезентативности (m) является важнейшей статистической величиной, необходимой для оценки достоверности результатов исследования. Это ошибка возникает в тех случаях, когда требуется по части охарактеризовать явление в целом. Эти ошибки неизбены. Они проистекают из сущности выборочного исследования; генеральная совокупность может быть охарактеризована по выборочной совокупности только с некоторой погрешностью, измеряемой ошибкой репрезентативности.
Ошибки репрезентативности нельзя смешивать с обычным представлением об ошибках: методических, точности измерения, арифметических и др.
Ошибки репрезентативности можно свести к достаточно малой величине, т.е. к величине допустимой погрешности. Делается это путем привлечения в выборку достаточного количества наблюдений (n).
при n 

при n 
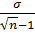
где mM– ошибка средней величины;
σ – среднее квадратическое отклонение;
n – число наблюдений.
Из данной формулы следует, что величина средней ошибки средней арифметической прямо пропорциональна степени разнообразия признака и обратно пропорциональна степени корню квадратному из числа наблюдений. Следовательно, уменьшение величины этой ошибки при определении степени разнообразия (σ) возможно путем увеличения числа наблюдений.
На этом принципе основан метод определения достаточного числа наблюдений для выборочного исследования.
Относительные величины (P), полученные при выборочном исследовании, также имеют свою ошибку репрезентативности, которая называется средней ошибкой относительной величины и обозначается mP.
Для определения средней ошибки относительной величины (P) используется следующая формула:
mP =
где P – относительная величина. Если показатель выражен в процентах, то q = 100-P, если P в промиллях, то q = 1000-P, если P – в продецимиллях, тоq = 10000-P,и т.д.; n – число наблюдений. При числе наблюдений менее 30 в знаменатель следует взять n-1.
mP =
2.3. Определение доверительных границ M и P.
Определяя для средней арифметической или (относительной ) величины два крайних значения: минимально возможное и максимально возможное, находят пределы, в которых может быть искомая величина генерального параметра. Эти пределы называют доверительными границами.
Доверительные границы средней арифметической в генеральной совокупности определяют по формуле:
Mген. = Mвыб. 
где Mген. –средняя величина признака в генеральной совокупности,
Mиыб.-средняя величина, полученная в результате исследованиявыборочной совокупности
tmM= 
Доверительные границы относительной величины в генеральной совокупности определяют по следующей формуле:
Pген. = Pвыб. 
гдеPген. – показатель в генеральной совокупности,
Pиыб.-средняя величина,показатель, полученный в результате исследования выборочнойсовокупности,
tmp 
Понятие «вероятность безошибочного прогноза» (P) – это вероятность, с которой можно утверждать, что в генеральной совокупности Mбудет находиться в пределах M 

Если n 

Для абсолютного большинства медицинских исследований степень вероятности безошибочного прогноза (P) должна быть не менее 95 %.
Значения критерия Стьюдента (t)
| K = n – 1 | ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ (P) | |
| 95.5 % (0.95) | 99.7 % (0.99) | 99.9 % (0.999) |
| 12,70 4,30 3,18 2,78 2,57 2,42 2,36 2,31 2,26 2,23 2,20 2,16 2,14 2,13 2,12 2,11 2,10 2,09 2,09 2,08 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,04 2,04 | 63,56 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,06 3,01 2,98 2,95 2,92 2,90 2,88 2,86 2,84 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,76 | 36,59 31,60 12,94 8,61 6,86 5,96 5,31 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,96 3,92 3,88 3,85 3,82 3,79 3,77 3,75 3,73 3,71 3,69 3,67 3,66 3,64 |
2.4. Определение достоверности разности средних (M) или относительных (P) величин по критерию t.
В медицине и здравоохранении по разности параметров оценивают средние и относительные величины, полученные для разных групп населения по полу, возрасту, а также групп больных и здоровых и т.д. Во всех случаях при сопоставлении двух сравниваемых величин возникает необходимость не только определить их разность, но и оценить ее достоверность.
Достоверность разности величин, полученных при выборочных исследованиях, означает, что вывод об их различии может быть перенесен на соответствующие генеральные совокупности.
Достоверность выборочной разности измеряется доверительным критерием (критерием точности t), который рассчитывается по специальным формулам для средних и относительных величин.
Формула оценки достоверности разности сравниваемых средних величин такова:
t= 
и для относительных величин:
t= 
где M1,M2, P1, P2 – параметры, полученные при выборочных исследованиях; m1 и m2– их средние ошибки; t – критерий точности. Разность достоверна при t 
Для большинства исследований, проводимых в медицине и здравоохранении, такая степень вероятности является вполне достаточной.
2.5. Оценка достоверности различия сравниваемых групп по критерию соответствия X 2 (хи-квадрат).
Определяя с помощью X 2 (хи-квадрат)соответствие эмпирического распределения теоретическому оценивают достоверность различия между выборочными совокупностями.
Критерий X 2 (в отличие от критерия t) применяется в тех случаях, когда нет необходимости знать величину того или иного параметра (среднюю или относительный показатель) и требуется оценить достоверность различия не только двух, но и большего числа групп.Х 2
Так, критерий X 2 (хи-квадрат) может быть использован для ответа на следующие вопросы: существенно ли отличаются друг от друга группы вакцинированных и невакцинированных по распределению их на больных и здоровых (т. е. эффективна ли вакцина); существенно ли отличаются группы населения с разным среднедушевым доходом по распределению их на больных и здоровых (т. е. влияет ли материальное обеспечение на уровень заболеваемости) и т. п.
Критерий X 2 (хи-квадрат) определяется по формуле:
X 2 = 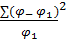
Где 

Определение критерия соответствия X 2 основано на расчете разницы между фактическими и ожидаемыми данными. Чем больше это разность (φ – φ1), тем с большей вероятностью можно утверждать, что существуют различия в распределении сравниваемых выборочных совокупностей и, наоборот, чем меньше разность (φ – φ1), тем меньше шансов на то, что сравниваемые выборочные совокупности различны между собой.