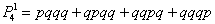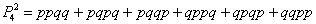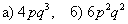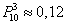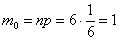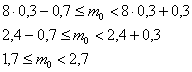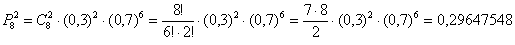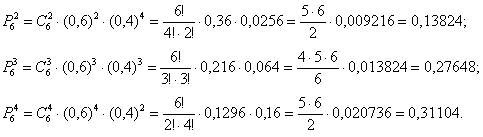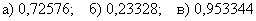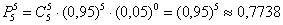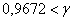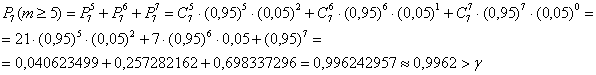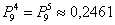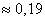Что понимают под испытанием математика
Математика — онлайн помощь
Как любая наука, теория вероятностей имеет свои исходные понятия, через которые определяются другие понятия. К основным понятиям теории вероятностей относятся: испытание, событие, вероятность события.
Изучение явлений происходит путем наблюдений и опытов, проводимых при определенных условиях. Испытанием в теории вероятностей называется осуществление какого-либо комплекса условий, при котором наблюдается данное явление. Предполагается, что данный комплекс условий может быть воспроизведен сколь угодно большое число раз. Итак, в теории вероятностей вместо слов “произведено наблюдение при осуществлении определенного комплекса условий” говорят кратко “произведено испытание”.
Событием называется всякий факт, который может наступить в результате испытания.
События можно классифицировать по степени возможности их появления и по характеру взаимосвязи.
Достоверным называется событие, которое в данном испытании всегда наступает, его обозначают 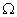
Невозможным называется событие, которое в данном испытании никогда не наступает, его обозначают 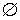
Случайным называется событие, которое в данном испытании может наступить, а может не наступить. Случайные события обозначают заглавными буквами латинского алфавита А, В, С,…
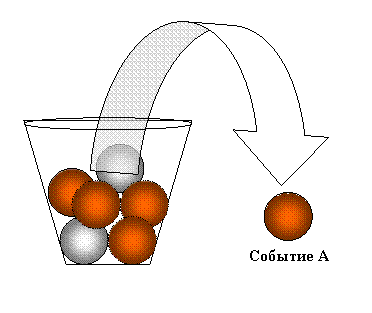
События называются несовместными, если появление одного из них исключает появление других событий в данном испытании. В противном случае события называются совместными. Примеры несовместных событий: появление герба и цифры при одном бросании монеты, попадание и промах при одном выстреле. Те же попадание и промах при двух выстрелах являются уже совместными событиями.
Несколько событий образуют полную группу событий, если в результате испытания обязательно наступит хотя бы одно из них. В частности, если события образуют полную группу и несовместны, то в результате испытания появится одно и только одно из этих событий.
Суммой событий 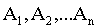
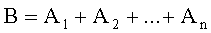
Произведением событий его обозначают 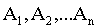
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
ИСПЫТАНИЕ
Смотреть что такое «ИСПЫТАНИЕ» в других словарях:
ИСПЫТАНИЕ — ИСПЫТАНИЕ, испытания, ср. (книжн.). 1. только ед. Действие по гл. испытать, проверка, исследование каких нибудь качеств, пригодности к чему нибудь. Испытание материалов. Испытание двигателя. Отправить в госпиталь на испытание. Быть на испытании.… … Толковый словарь Ушакова
испытание — Определение одной или нескольких характеристик согласно установленной процедуре. [ГОСТ Р ИСО 9000 2008] испытание Экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как результата воздействия … Справочник технического переводчика
ИСПЫТАНИЕ — понятие теории вероятностей. Испытание может иметь один (и только один) из n исходов. Каждый исход испытания рассматривается как случайное событие, имеющее определенную вероятность … Большой Энциклопедический словарь
испытание — ИСПЫТАНИЕ, диагностика, опробование, проба, проверка, тест ИСПЫТЫВАТЬ/ИСПЫТАТЬ, несов. и сов. диагностировать, сов. опробовать, проверять/проверить, несов. и сов. тестировать … Словарь-тезаурус синонимов русской речи
Испытание — – определение одной или нескольких характеристик согласно установленной процедуре. [ГОСТ Р ИСО 9000 2008] Испытание – экспериментальное определение количественных и (или) качественных характеристик свойств объекта испытаний как… … Энциклопедия терминов, определений и пояснений строительных материалов
Испытание — А. Проверка качества или заявленных свойств предмета. Б. Контрольный опрос, экзамен, тест. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
ИСПЫТАНИЕ — ИСПЫТАНИЕ, я, ср. 1. см. испытать. 2. Проверочный опрос или экзамен. Приёмные испытания. 3. Тягостное переживание, несчастье. Тяжёлое и. Суровые испытания войны. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Испытание — Братья, Драупади и Кунти уже не чаяли увидеть Арджуну, считая его погибшим, когда он в диадеме, сверкающей драгоценными камнями, опустился прямо с неба на колеснице в их объятья. И не было им конца. После того как все насытились радостью… … Энциклопедия мифологии
ИСПЫТАНИЕ — на прочность. Публ. Проверка сил, выдержки, выносливости человека в экстремальных ситуациях. Ф 1, 225; Мокиенко 2003, 38 … Большой словарь русских поговорок
Испытание — техническая операция, заключающаяся в установлении характеристик продукции, процесса или услуги … Российская энциклопедия по охране труда
Основные понятия теории вероятностей
Что нужно знать
Это самая первая, вводная статья по теории вероятностей. Сама наука является достаточно самостоятельным разделом математики, и, чтобы понять её основы (а также для того, чтобы научиться решать простейшие задачи вроде задания 4 из ЕГЭ), нужно лишь уметь совершать арифметические действия с числами и дробями. Так что, если вам тяжело даются логарифмы и тригонометрия или совершенно непонятна производная, это никак не помешает вам разобраться в теории вероятностей.
Что вы узнаете
Что такое испытание и исход
Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание. Вообще говоря, эксперимент должен быть повторяемым. То есть, чтобы мы могли говорить о вероятности, у нас должна быть возможность провести эксперимент не один (а если совсем строго, то сколько угодно) раз.
Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: <выпало 6 6 6 > и <выпало не 6 6 6 >, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).
На столе лежит колода карт, а мы вытягиваем оттуда одну карту. Это пример случайного испытания. У этого испытания 5 2 52 5 2 исхода, так как мы можем вытянуть любую из 5 2 52 5 2 карт (в каждой из четырех мастей 1 3 13 1 3 карт от двойки до туза).
Бросок обыкновенного игрального кубика является классическим примером испытания. Сколько исходов возможно у этого испытания?
Важно понимать, что список возможных результатов мы очерчиваем сами (исходя из «здравого смысла»). Так, при броске монеты мы считаем «возможным», что она упадёт вверх аверсом («орлом») или вверх реверсом («решкой»), просто не рассматривая возможности того, что монета встанет на ребро, будет проглочена пролетающей птицей и т.п. В то же время мы считаем несущественным, упадёт монета на стол или на пол, со звоном или бесшумно и пр.; мы ограничили себя двумя интересующими нас исходами.
Рассмотрим чуть более сложный пример: мы одновременно подкинули монету и бросили игральный кубик. Сколько (и каких) исходов у этого испытания?
Для ответа на этот вопрос попробуем составить список результатов. Для монеты: Орёл (О) и Решка (Р). Для кубика: 1, 2, 3, 4, 5, 6. А теперь посмотрим, что может быть с кубиком, если монета выпала на Орла? Но ведь кубику в некотором смысле «всё равно», как выпала монета (в теории вероятностей это называется «независимые события», но об этом позже). То есть для него по-прежнему возможны все 6 вариантов. То же самое и если она выпала на Решку. Значит, можно перечислить все возможные исходы подряд, в виде «результат монеты» — «результат кубика». Сделаем это:
| О — 1 | О — 2 | О — 3 | О — 4 | О — 5 | О — 6 | всего 6 |
| Р — 1 | Р — 2 | Р — 3 | Р — 4 | Р — 5 | Р — 6 | всего 6 |
Представим следующее испытание: два игральных кубика бросают одновременно. Сколько исходов будет в этом случае?
Что такое случайное событие
Случайное событие — это подмножество множества исходов испытания.
Из скольки исходов состоит случайное событие «выпал дубль» (то есть одинаковые числа на кубиках) при испытании «бросание двух кубиков одновременно»?
Попробуйте ответить на вопрос посложнее:
Из скольки исходов состоит случайное событие «сумма очков на двух кубиках меньше 4»? Испытание то же — два кубика бросают одновременно.
Как считать вероятность события
Исходы, входящие в событие, называются благоприятными для этого события.
Прежде чем перейти к классическому определению вероятности, заметим, что для его применения требуется выполнение определённого условия — равновозможности всех исходов. Это условие может быть недостаточно строго определено, но интуитивно оно понятно. Например, если в качестве исходов при бросании монеты выбрать «орёл», «решка» и «ребро», то классическое определение вероятности применять нельзя, так как шансы на последний исход меньше, чем на первые два. А если выбрать только «орёл» и «решка», то можно — ведь нет никаких оснований считать один исход более частым, чем другой.
Итак, пусть у нас есть испытание с определённым набором равновозможных исходов. Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.
P < Событие A >= Число исходов, благоприятных для A Общее число исходов P\<\text<Событие >A\>=\frac <\text<Число исходов, благоприятных для >A><\text<Общее число исходов>> P < Событие A >= Общее число исходов Число исходов, благоприятных для A
Конечно, «в жизни» в основном встречаются ситуации, когда одни исходы встречаются чаще других, и тогда нужно использовать скорректированное определение вероятности. Но в школьных задачах исходы всегда одинаково ожидаемы, так что для нахождения вероятности нужно только правильно посчитать количество исходов, входящих в событие, и общее количество исходов испытания, после чего поделить одно на другое.
Рассмотрим пример. Из стандартной колоды карт (от двойки до туза) наугад вытащили одну карту. Какова вероятность, что эта карта — с цифрой?
Чему равна вероятность достоверного события?
Попробуйте решить несложную задачу, чтобы убедиться, что всё понятно.
В классе 21 человек, среди них 2 Саши. Классный руководитель назначил дежурной Настю и случайным образом выбирает ей напарника. Какова вероятность, что напарником окажется Саша? (Запишите ответ в виде десятичной дроби.)
Эту статью написал для вас Сергей Вальковский, учитель математики Центра образования «Пятьдесят седьмая школа», Москва.
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №33. Вероятность события. Сложение вероятностей.
Перечень вопросов, рассматриваемых в теме:
— события, испытания, вероятность, случайное событие, невозможного и достоверного события;
— понятие классической вероятности события;
— поиск вероятности случайного события, пользуясь определением классической вероятности;
— поиск вероятности суммы событий.
Испытанием называется осуществление определенных действий.
Событие— факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
Пространство элементарных событий Ω — множество всех различных исходов произвольного испытания.
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Её ещё называют статистической вероятностью события.
Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 180-188.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
В корзине лежат клубки ниток зеленого и белого цвета. Бабушка просит внучку достать ей клубок ниток и, внучка наугад из корзины вынимает один клубок. Какое из следующих событий может произойти?
1) вынутый предмет окажется клубком
2) вынутый предмет окажется красным клубком
3) вынутый предмет окажется зеленым клубком
4) вынутый предмет не окажется клубком
Ответ: первое и третье.
1. Теория вероятностей – раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними. Рассмотрим некоторые ключевые понятия, которые используются в теории вероятностей.
Испытанием называется осуществление определенных действий.
Под событием понимают любой факт, который может произойти в результате испытания.
Любой результат испытания называется исходом.
Достоверным называют событие, которое в результате испытания обязательно произойдёт.
Невозможным называют событие, которое заведомо не произойдёт в результате испытания.
События обычно обозначаются заглавными буквами латинского алфавита (А, В, С, D,…).
Рассматривая приведенный пример, мы можем сформулировать следующие заключения.
2. Определим еще несколько важных понятий теории вероятностей
Пространство элементарных событий Ω— множество всех различных исходов произвольного испытания.
Например, при броске одной игральной кости пространство элементарных событий Ω=
Если события не могут произойти одновременно в одном испытании, то события называются несовместными.
Например, при бросании монеты не могут одновременно выпасть «Орёл» и «Решка».
Простейшим примером несовместных событий является пара противоположных событий.
Противоположное событие происходит тогда, когда исходное событие А не происходит.
Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.
Полной группой событий называется такая система событий, что в результате испытания непременно произойдет одно и только одно из них.
Монету подбросили дважды. Укажите все элементарные события полной группы событий.
Элементарными событиями являются:
— Выпал один «орел» и одна «рещка».
3. Чтобы выяснить, насколько вероятно то или иное случайное событие, нужно подсчитать, как часто оно происходит.
Число испытаний, в которых событие наступило, назовем абсолютной частотой и обозначим n. Общее число произведенных испытаний обозначим N.
Отношение абсолютной частоты к числу испытаний n/N называется относительной частотой события.
Относительная частота показывает, какая доля испытаний завершилась наступлением данного события. Эта относительная частота и определяет вероятность случайного события. Ее еще называют статистической вероятностью события.
Статистическая вероятность события рассчитывается опытным путем.
Еще со времен Древнего Китая за 2238 лет до нашей эры на основании метрик демографы обнаружили, что на каждую тысячу новорожденных приходится 514 мальчиков.
Это означает, что Вероятность рождения мальчика составляет 0,514.
1. Классическое определение вероятности применяется для равновозможных событий.
К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.
Например, при бросании игрального кубика события выпадения любого из очков равно возможны.
Рассмотрим произвольный эксперимент.
Пусть n— число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов. Тогда вероятностью события А называется число
Согласно определению вероятности наименьшее значение вероятности принимает невозможное событие, так как оно не может наступить и для него m=0, значит и вероятность равна 0.
Наибольшее значение принимает достоверное событие. В силу того, что оно гарантированно произойдет, для него m=n, Р=m/n=n/n=1.
Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.
Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:
Примеры и разбор решения заданий тренировочного модуля
Известна история о том, как однажды к Г. Галилею явился солдат и попросил помочь ему в решении насущного вопроса: какая сумма 9 или 10 очков при бросании трех костей выпадает чаще?
Может показаться, что шансы равны, так как каждая сумма из 9 и 10 очков может быть получена одним их шести способов:
9 = 1 + 2 + 6 = 1 + 3 + 5 = 1 + 4 + 4 = 2 + 2 + 5 = 2 + 3 + 4 = 3 + 3 + 3;
10 = 1 + 3 + 6 = 1 + 4 + 5 = 2 + 2 + 6 = 2 + 3 + 5 = 2 + 4 + 4 = 3 + 3 + 4.
Однако с учетом перестановок для суммы 9 очков получается 25 различными способами (по 6 способов для первого, второго, пятого вариантов суммы, по 3 способа для третьего и четвертого вариантов, 1 способ для последнего варианта 6 + 6 + 3 + 3 + 6 + 1), а для суммы 10 очков – 27 различными способами (6 + 6 + 3 + 6 + 3 + 3). Как видно, шансы этих случайных событий довольно близки между собой и относятся друг к другу как 25:27, что и вызвало затруднения солдата.
Таким образом, чаще выпадает сумма 10.
Пример 2. В средние века среди феодальной знати были широко распространены азартные игры. Большим любителем таких игра был француз шевалье де Мере. Страстного игрока в кости, придворного французского короля шевалье де Мере можно отнести к числу «основателей» теории вероятностей. Заслуга его состоит в том, что он настойчиво заставлял математиков решать различные задачи, на которые наталкивался сам во время своей практики игры. Он хотел разбогатеть при помощи игры в кости. Для этого шевалье придумывал различные усложненные правила игры. Страстному игроку, но плохому математику, де Мере посчастливилось иметь такого друга, как Паскаль. В 1654 г. шевалье де Мере обратился к Блезу Паскалю за помощью в разрешении проблем, связанных с вероятностью благоприятных результатов при бросании игральных костей.
Одна из задач была поставлена следующим образом: Игральная кость бросается четыре раза. Шевалье бился об заклад, что при этом хотя бы один раз выпадет шесть очков. Какова вероятность выигрыша для шевалье? Ответ округлите до десятых.
Так как при каждом бросании игральной кости имеется 6 различных возможностей, то при четырех бросаниях кости число различных возможных случаев будет 6 · 6 · 6 · 6 = 1296.
Среди этих 1296 случаев будет 5 · 5 · 5 · 5 = 625 таких, где шестерка не выпадет ни разу.
В 1296 – 625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Следовательно, вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна 671/1296, что чуть больше 0,5.
Независимые испытания и формула Бернулли
Сегодня на уроке мы познакомимся с ещё одним распространённым следствием теорем сложения и умножения вероятностей, которое касается независимых испытаний, и рассмотрим многочисленные примеры на использование формулы Бернулли. Данная задача входит в «обязательный комплект» типовой самостоятельной/контрольной работы по теории вероятностей, поэтому ваше ближайшее времяпровождение будет крайне полезным. Кроме того, я расскажу, в чём заблуждается подавляющее большинство участников лотерей и азартных игр. …Нееет, вера или слабая надежда «сорвать куш» тут совершенно ни при чём 😉 Не успев и глазом моргнуть, погружаемся в тему:
Что такое независимые испытания? Практически всё понятно уже из самого названия. Пусть производится несколько испытаний. Если вероятность появления некоего события 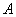
Простейшие примеры:
– монета подбрасывается 10 раз;
– игральная кость подбрасывается 20 раз.
Совершенно ясно, что вероятность выпадения орла либо решки в любом испытании не зависит от результатов других бросков. Аналогичное утверждение, естественно, справедливо и для кубика.
А вот последовательное извлечение карт из колоды не является серией независимых испытаний – как вы помните, это цепочка зависимых событий. Однако если карту каждый раз возвращать обратно, то ситуация станет «такой, какой надо».
Спешу обрадовать – у нас в гостях очередной Терминатор, который абсолютно равнодушен к своим удачам/неудачам, и поэтому его стрельба представляет собой образец стабильности =):
Стрелок совершает 4 выстрела по мишени. Вероятность попадания при каждом выстреле постоянна и равна 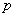
а) стрелок попадёт только один раз;
б) стрелок попадёт 2 раза.
Решение: условие сформулировано в общем виде и вероятность попадания в мишень при каждом выстреле считается известной. Она равна 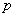
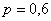
Коль скоро мы знаем 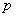
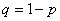
а) Рассмотрим событие «Стрелок попадёт только один раз» и обозначим его вероятность через 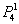
По теоремам сложения вероятностей несовместных и умножения вероятностей независимых событий:
Внимание! Если вам НЕ ПОНЯТНА эта запись, пожалуйста, вернитесь к предыдущему уроку по вышеприведённой ссылке!
Упростим результат с помощью комбинаторной формулы количества сочетаний:
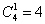
И, поскольку в каждом случае имеет место 1 попадание и 3 промаха, то:
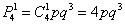
…Как-то так «с лёгкой руки» я начал называть повторные независимые испытания «попытками», что не в каждой задаче может быть корректным… …ну да ладно.
б) Рассмотрим событие «Стрелок попадёт два раза» и обозначим его вероятность через 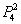
в 1-й и 2-й попытках
или
в 1-й и 3-й попытках
или
в 1-й и 4-й попытках
или
во 2-й и 3-й попытках
или
во 2-й и 4-й попытках
или
в 3-й и 4-й попытках.
Таким образом, по тем же теоремам сложения и умножения вероятностей:
Можно ли так решать задачу? Безусловно, можно. Но что делать, если серия состоит из 5, 6 или бОльшего количества выстрелов? Тут уже будут получаться десятки слагаемых, запись которых отнимет много времени и места. В этой связи рациональнее придерживаться более компактной схемы:
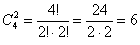
И, поскольку в любом исходе ровно 2 попадания и 2 промаха, то:
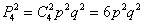
Ответ:
Итак – вероятность того, что будет 1 попадание из 4, равна 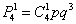
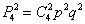
Только что на конкретном примере мы повторили путь Якоба Бернулли, который несколько веков назад вывел формулу, названную позже в его честь:
– Вероятность 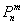
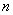
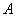
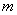
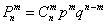
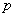
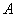
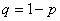
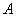
Коэффициент 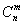
Примечание: формула Бернулли справедлива только для тех независимых испытаний,
в которых вероятность 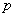
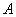
За примером далеко ходить не будем:
Найти вероятность того, что при 10 бросках монеты орёл выпадет 3 раза.
Решение: сначала немного порассуждаем: всего проводится 10 повторных независимых испытаний. Сколькими способами можно выбрать 3 испытания, в которых выпадет орёл?
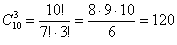
Это что же получается – записывать 120 слагаемых, в каждом из которых 10 множителей? =)
Используем формулу Бернулли: 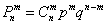
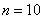
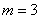
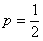
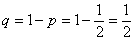
Таким образом:
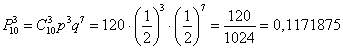
Ответ:
Следует отметить, что повторный характер независимых испытаний не является «жизненно важным» (необходимым) условием для применения формулы Бернулли. Рассмотрим похожую задачу (которая, кстати, эквивалентна Задаче 8 урока о классическом определении вероятности):
Найти вероятность того, что при броске 10 монет орёл выпадет на 3 монетах.
Здесь испытания не повторяются, а скорее, производятся одновременно, но, тем не менее, работает та же самая формула: 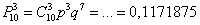
Решение будет отличаться смыслом и некоторыми комментариями, в частности:
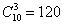
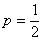
и т.д.
Однако на практике подобные задачи встречаются не столь часто, и, видимо, по этой причине формула Бернулли чуть ли не стереотипно ассоциируется только с повторными испытаниями. Хотя, как только что было показано, повторяемость вовсе не обязательна.
Следующая задача для самостоятельного решения:
Игральную кость бросают 6 раз. Найти вероятность того, что 5 очков:
а) не выпадут (выпадут 0 раз);
б) выпадут 2 раза;
в) выпадут 5 раз.
Результаты округлить до 4 знаков после запятой.
Краткое решение и ответ в конце урока.
Очевидно, что в рассматриваемых примерах некоторые события более вероятны, а некоторые – менее вероятны. Так, например, при 6 бросках кубика даже безо всяких расчётов интуитивно понятно, что вероятности событий пунктов «а» и «бэ» значительно больше вероятности того, что «пятёрка» выпадет 5 раз. А теперь поставим задачу найти
НАИВЕРОЯТНЕЙШЕЕ число появлений события  в
в  независимых испытаниях
независимых испытаниях
Опять же на уровне интуиции в Задаче №3 можно сделать вывод о том, что наивероятнейшее количество появлений «пятёрки» равно единице – ведь всего граней шесть, и при 6 бросках кубика каждая из них должна выпасть в среднем по одному разу. Желающие могут вычислить вероятность 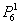
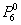
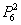
Сформулируем строгий критерий: для отыскания наивероятнейшего числа 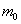
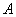
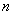
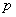
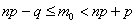
1) если значение 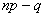
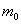
в частности, если 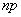
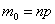
2) если же 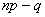
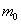
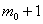
Наивероятнейшее число появлений «пятёрки» при 6 бросках кубика подпадает под частный случай первого пункта:
В целях закрепления материала решим пару задач:
Вероятность того, что при броске мяча баскетболист попадёт в корзину, равна 0,3. Найти наивероятнейшее число попаданий при 8 бросках и соответствующую вероятность.
А это уже если и не Терминатор, то, как минимум, хладнокровный спортсмен =)
Решение: для оценки наивероятнейшего числа попаданий используем двойное неравенство 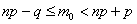
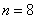
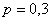
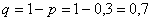
Таким образом, наивероятнейшее количество попаданий при 8 бросках находится в следующих пределах:
Поскольку левая граница – дробное число (пункт №1), то существует единственное наивероятнейшее значение, и, очевидно, что оно равно 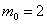
Используя формулу Бернулли 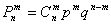
Ответ: 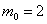
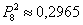
Аналогичное задание для самостоятельного решения:
Монета подбрасывается 9 раз. Найти вероятность наивероятнейшего числа появлений орла
Примерный образец решения и ответ в конце урока.
А сейчас весьма любопытная ситуация: предположим, что во всех 9 испытаниях выпал орёл. Это, кстати, не являются каким-то уж сильно невероятным событием: 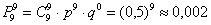
Вопрос: какая сторона монеты вероятнее всего выпадет в 10-м испытании?
Решка? Глубокое заблуждение!
Правильный ответ: вероятности останутся равными! Почему? Причина была сформулирована ещё в самом начале урока: поскольку испытания независимы, то вероятность выпадения орла либо решки в любом испытании не зависит от результатов других испытаний!
Однако игры разума таковы, что у многих людей напрашивается следующий вывод: «раз орёл выпал много раз подряд, то теперь выпадение решки гораздо (!) вероятнее». В теории и на практике этот психологический феномен получил название «Ошибка игрока». Если подбрасывать монету тысячи, десятки тысяч раз, то соотношение орлов/решек будет примерно равным (о чём мы ещё поговорим в статье Статистическое определение вероятности). Но в этом процессе неоднократно встретятся эпизоды, когда монету «заклинит» на какой-то одной грани; и КАК ИМЕННО распределятся эти «необычные» случаи на длинной дистанции – никто не знает.
К слову, о «необычности». Любая случайная последовательность девяти орлов/решек так же вероятна, как и выпадение 9 орлов! Проверить данный факт легче лёгкого: запишем произвольную последовательность исходов, например:
Орёл/Решка/Решка/ Орёл /Решка/ Орёл /Решка/ Орёл /Орёл
По теореме умножения вероятностей независимых событий, вероятность появления этой цепочки: 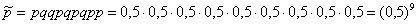
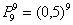
И здесь мы сталкиваемся со второй иллюзией – человек склонен считать «красивые» комбинации чем-то из ряда вон выходящим и чуть ли не фантастическим. Но на самом деле ничего «необычного», например, в комбинации О/О/О/Р/Р/Р/О/О/О – нет, и она может запросто появиться в серии испытаний. Вероятность получить, скажем, пиковый «Ройял-флеш» в покере составляет 1:2598960, однако мало кто задумывается, что с той же вероятностью приходит ЛЮБАЯ, в том числе, совершено «мусорная» комбинация из пяти карт! И с этой точки зрения «сверхъестественная» комбинация 10, В, Д, К, Т пик ничем не примечательна – встречалась «в истории» наряду с другими очень много раз.
Кстати, к теме нашего разговора относятся и типичные ситуации в карточных играх – когда «карта идёт» и наоборот – когда «постоянно сдают один мусор» или «фатально не везёт». Такие «полосы» бывают у каждого игрока, и никакой мистики в этом нет.
На просторах Интернета часто встречается популярный «секрет выигрыша» в рулетку, также известный под названием «Мартингейл». Примерная суть состоит в следующем: «Ставьте на красное. Если выпало чёрное, удваивайте ставку и снова ставьте на красное. Если снова выпало чёрное, то ещё раз удваивайте ставку и снова ставьте на красное и т.д.». Казалось бы – вот оно, золотое дно, ведь красных секторов целых 18 из 37 (18 черных и 1 зеро в европейской рулетке)! И уж «красное» должно выпасть если не на 5-й, то на 10-й раз точно, что позволит отыграть всё ранее поставленное с прибылью!
Ничего подобного! Вероятность выпадения красного сектора в любом испытании постоянна 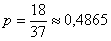
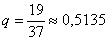
Остаётся вопрос: так почему же этот «удивительный способ» рекламируется в Сети на каждом шагу? Ответ прост: казино распиливает с владельцем сайта-лохотрона проигранные деньги каждого привлечённого Буратино. И что совсем забавляет – «благодетель» просит, чтобы особо везучие лохи отблагодарили его материально (обычно депозит сливается далеко не сразу и поначалу можно даже неплохо подняться). Кто виноват? Конечно же, мошенническая «шарашка», которая специально настроила программное обеспечение на «невероятный» проигрыш. Что делать? Попытать удачи в других заведениях.
«Ошибка игрока» совершается и многими участниками лотерей. На сайте одной лотереи на самом видном месте расположена информация о том, «какие номера давно не выпадали». И вот – целая армия энтузиастов начинает собирать статистику тиражей, подгадывать определённые комбинации и т.д. Чистой воды химера и пустая трата времени – если, например, №8 не выпадал 50 раз подряд, то он с таким же успехом может не выпасть ещё 150 розыгрышей (это не ирония – я в прямом смысле). Однако если провести десятки тысяч тиражей, то количество появлений всех номеров будет примерно равным. Но В КАКОМ ПОРЯДКЕ И КАКИМИ СЕРИЯМИ будет выпадать та же «восьмёрка» на длинной дистанции – никто предсказать не может.
«Русское лото» в этом смысле честнее – оно призывает «поставить на любимые номера», т.е. приобрести билет (онлайн), в котором присутствуют понравившиеся числа.
Но в действительности нет никакой разницы – покупаете ли вы билет наугад, или выбираете билет с определёнными числами, или даже если заполняете бланк самостоятельно. Это если не учитывать потусторонние силы =)
После увлекательного отступления рассмотрим ещё несколько задач, а затем я поделюсь секретом правильной игры в азартные игры и лотереи.
Среди изделий, произведенных на станке-автомате, в среднем бывает 60% изделий первого сорта. Какова вероятность того, что среди 6 наудачу отобранных изделий будет:
а) от 2 до 4 изделий первого сорта;
б) не менее 5 изделий первого сорта;
в) хотя бы одно изделие более низкого сорта.
Вероятность производства первосортного изделия не зависит от качества других выпущенных изделий, поэтому здесь идёт речь о независимых испытаниях. Старайтесь не пренебрегать анализом условия, а то может статься – события-то зависимые или задача вообще о другом.
Решение: вероятность зашифрована под проценты, которые, напоминаю, нужно разделить на сто: 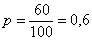
Тогда: 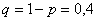
а) Событие «Среди 6 наудачу отобранных изделий будет от 2 до 4 изделий первого сорта» состоит в трёх несовместных исходах:
среди 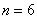
С исходами удобнее разделаться по отдельности. Трижды используем формулу Бернулли 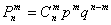
По теореме сложения вероятностей несовместных событий:
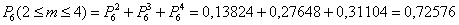
Решение можно было записать и «одной строкой», что мы, впрочем, сделаем в следующем пункте:
б) Событие «Среди 6 наудачу отобранных изделий будет не менее 5 изделий первого сорта» состоит в 2 несовместных исходах: первосортных изделий будет пять или шесть.
По теореме сложения вероятностей несовместных событий: 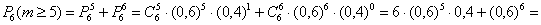
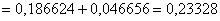
в) Вероятность того, что «Среди 6 наудачу отобранных изделий будет хотя бы одно изделие более низкого сорта» удобно найти через вероятность противоположного события («Все изделия будут первосортными»), которая уже известна:
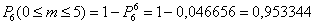
Ответ:
Давайте заодно вспомним такое полезное понятие, как полная группа событий. Что осталось не найденным? Остались не найденными вероятности двух событий.
Не знаю кому как, а мне порядком поднадоел микрокалькулятор, и я предлагаю воспользоваться расчётным макетом по теории вероятностей – это подарок для самых прилежных студентов, которые не уходят курить во время моих занятий =)
Вводим исходные данные и получаем:
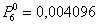
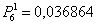
Проверка: 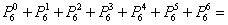
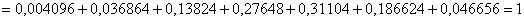
что и требовалось проверить.
Небольшое задание для самостоятельного решения:
Производится 8 выстрелов по цели, в каждом из которых вероятность попадания равна 0,1. Найти вероятность того, что цель будет поражена хотя бы два раза.
Краткое решение и ответ в конце урока.
Следует отметить, что задачи на формулу Бернулли «хорошо узнаются» и обычно не вызывают затруднений. С дополнительными, в том числе весьма интересными примерами по теме можно ознакомиться в этой pdf-ке с готовыми решениями. И одну из таких задач я разберу в заключение урока:
Для нормальной работы вычислительного центра необходима безотказная работа в течение дня, как минимум, 5 компьютеров. Сколько компьютеров нужно установить, чтобы с вероятностью, не меньшей 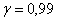
Решение: из условия легко найти, что вероятность безотказной работы любого компьютера в течение дня составляет 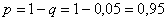
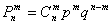
Поскольку для нормальной работы центра необходима безотказная работа, как минимум, 5 компьютеров, то может быть пяти и хватит?
1) Если в вычислительном центре установить 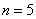
Но по условию нормальную работу центра нужно обеспечить с вероятностью, не меньшей, чем 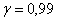
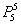
2) Предположим, что в вычислительном центре установлено 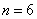
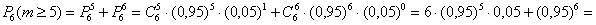
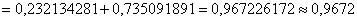
Данное значение нас тоже не устроит, так как оно меньше требуемой надёжности работы вычислительного центра:
Таким образом, шести компьютеров тоже не достаточно. Добавляем ещё один:
3) Пусть в вычислительном центре 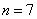
Есть! Требуемый уровень надёжности достигнут.
Можно, конечно, поставить и бОльшее количество компьютеров, но зачем переплачивать? =)
Ответ: чтобы обеспечить нормальную работу вычислительного центра в течение дня с вероятностью, не меньшей 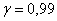
Формула Бернулли очень удобна, но с другой стороны, обладает и рядом недостатков. Так, например, при достаточно больших значениях «эн» и «эм» её применение затруднено ввиду огромных значений факториалов. В этом случае используют теоремы Лапласа, которые мы рассмотрим на следующем уроке. Другая распространённая на практике ситуация – когда вероятность 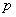
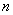
И, наконец, обещанный секрет:
…Так всё-таки – как правильно играть в азартные игры и лотереи?
Наверное, многие ожидали услышать от меня что-нибудь вроде: «Лучше вообще не играть», «Открыть собственное казино», «Организовать лотерею» и т.п.
Ну почему же не играть? Игра – это одно из развлечений, а за развлечения, как известно, нужно… совершенно верно! Поэтому средства, на которые вы играете, следует считать платой за развлечение, но ни в коем случае трагической потерей.
Тем не менее, каждый участник азартной игры хочет выиграть. И выиграть хорошую сумму. Какой тактики (о стратегии речи не идет вообще) выгоднее всего придерживаться в игре с заведомо проигрышным математическим ожиданием, например, в рулетке? Лучше всего сразу поставить все фишки, как вариант, на «красное» либо «чёрное». С вероятностью 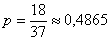
Не имеет смысла играть по какой-то «системе» (хотя бы потому, что это глупо) и тратить на это часы/дни/недели – в той же рулетке заведение имеет минимальное преимущество, и проигрываться можно ооооочень долго. Если в оффлайновом казино это ещё как-то можно понять (общение, выпивка, девочки и т.д.), то онлайн игра оставит вас с красными глазами и чувством глубокой досады.
Что касается лотерей, то билет лучше покупать опять же ради развлечения и… наобум. Или «по наитию». Правда, лично я почему-то никогда не слышал об экстрасенсах и предсказателях, которые выигрывают в лотереи =) Не иначе, как шифруются.
Естественно, перечисленные советы не относятся к хроническим лудоманам и им как раз таки «Лучше вообще не играть». Ну а тем посетителям, которые мечтают разбогатеть на гэмблинге, настоятельно рекомендую прочитать либо ещё раз перечитать вводную статью по теории вероятностей.
Задача 3: Решение: используем формулу Бернулли: 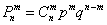
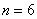
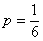
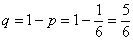
а) 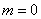
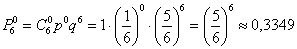
б) 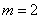
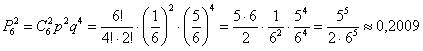
в) 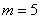
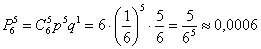
Ответ:
Задача 5: Решение: в данной задаче речь идёт о независимых испытаниях, при этом:
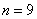
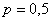
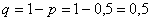
Найдём наивероятнейшее количество 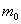
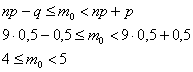
Так как 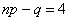
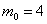
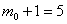
Используя формулу Бернулли, вычислим соответствующие вероятности: 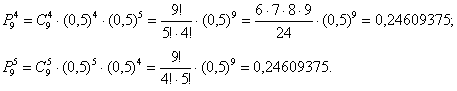
Ответ: 4 и 5;
Задача 7: Решение: используем формулу Бернулли: 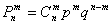
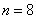
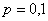
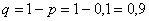
По теореме сложения вероятностей несовместных событий:
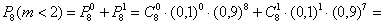
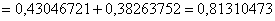
Найдём вероятность противоположного события:
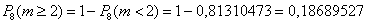
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5