Что понимают под моделью

Модель

Модель — это форма отображения определённого фрагмента действительности (предмета, явления, процесса, ситуации) — оригинала модели, которое содержит существенные свойства моделируемого объекта и может быть представлено в абстрактной (мысленной или знаковой) или материальной (предметной) форме. Модель обычно представляет собой либо материальную копию оригинала, либо некоторый условный образ, сконструированный для хранения и расширения знания (информации) об оригинале, конструирования оригинала, его преобразования или управления им. Таким образом, в общем случае под моделью обычно понимают некоторый объект, который каким-либо образом используется, чтобы представить что-то другое. Процедуры создания моделей широко используются как в научно-теоретических, так и в прикладных сферах человеческой деятельности.

В математической логике (см. Логика математическая) и математике под моделью понимается интерпретация каких-либо логико-математических положений и их систем. Изучение таких интерпретаций производится в логической семантике (см. Семантика), а также в теории моделей (см. Теория моделей) математической логики, где под моделью понимают произвольное множество элементов с определёнными на нём функциями и предикатами.

С точки зрения научного познания (см. Наука) модель — это «объект-подобие» или «объект-заместитель» объекта-оригинала в познании и практике, воспроизводящий определённые характеристики изучаемого оригинала. В этом смысле модель всегда соответствует объекту-оригиналу — в тех свойствах, которые подлежат изучению, но в то же время отличается от него по ряду других признаков, что делает модель удобной для исследования изучаемого объекта. Результаты разработки и исследования моделей при определённых условиях, принимаемых в методологии науки и специфических для различных областей и типов моделей, распространяются на оригинал. Возможны два способа конструирования модели: если первый способ подразумевает эмпирически выявленные свойства и связи объекта к его модели, то второй уже в исходной точке предполагает теоретическое воссоздание объекта в модели, и поскольку модель известна, то считается познаваемым и объект.

Изучение объекта-оригинала путём создания и исследования его модели, называется в методологии науки (см. Методология науки) методом моделирования или моделированием и представляет собой универсальный приём познания, который использовался ещё в глубокой древности, хотя и не осознавался в качестве особого метода исследования. Использование моделирования в научном познании диктуется необходимостью раскрыть такие стороны объектов, которые либо невозможно постигнуть путём непосредственного изучения, либо непродуктивно изучать их таким образом в силу каких-либо ограничений.

Модели, применяемые в научном познании, разделяются на два больших класса: материальные и идеальные. Первые являются природными объектами, подчиняющимися в своём функционировании естественным законам. Вторые представляют собой идеальные образования, зафиксированные в соответствующей знаковой форме и функционирующие по законам логики мышления, отражающей мир. Материальные модели подразделяются на два основных вида: предметно-физические и предметно-математические модели. Идеальные модели также подразделяются на два основных вида: идеализированные модельные представления и знаковые модели. Соответственно этому различению выделяют основные разновидности моделирования. Каждое из них применяется в зависимости от особенностей изучаемого объекта и характера познавательных задач.

Предметно-физическое моделирование широко используется как в научной практике, так и в сфере материального производства. Такое моделирование всегда предполагает, что модель должна быть сходна с оригиналом по физической природе и отличаться от него лишь численными значениями ряда параметров. Наряду с этим в практике научного исследования часто используется и такой вид моделирования, при котором модель строится из объектов иной физической природы, чем оригинал, но описывается одинаковой с ним системой математических зависимостей. В отличие от предметно-физического этот вид моделирования называют предметно математическим. Предметная модель становится здесь объектом испытания и изучения, в результате которого создаётся её математическое описание. Последнее затем переносится на моделируемый объект, характеризуя его структуру и функционирование.

В развитой науке, особенно при переходе к теоретическим исследованиям, широко используется моделирование с применением идеальных моделей. Этот способ получения знаний об объектах может быть охарактеризован как моделирование посредством идеализированных представлений. Он является ведущим инструментом теоретического исследования. Активно используя модельные представления, научное исследование вместе с тем применяет и так называемое знаковое моделирование, которое основано на построении и испытании математических моделей некоторого класса явлений, без использования при этом вспомогательного физического объекта, который подвергается испытанию. Последнее отличает знаковую модель от предметно-математической. Такой вид моделирования иногда называют также абстрактно-математическим. Он требует построения знаковой модели, представляющей некоторый объект, где отношения и свойства объекта представлены в виде знаков и их связей. Эта модель затем исследуется чисто логическими средствами, и новое знание возникает в результате дедуктивного развёртывания модели без обращения к предметной области, на основании которой выросла данная знаковая модель.

Источник

Модель

Построение и исследование моделей, то есть моделирование, облегчает изучение имеющихся в реальном устройстве (процессе, …) свойств и закономерностей. Применяют для нужд познания (созерцания, анализа и синтеза).

Моделирование является обязательной частью исследований и разработок, неотъемлемой частью нашей жизни, поскольку сложность любого материального объекта и окружающего его мира бесконечна вследствие неисчерпаемости материи и форм её взаимодействия внутри себя и с внешней средой.

Одни и те же устройства, процессы, явления и т. д. (далее — «системы») могут иметь много разных видов моделей. Как следствие, существует много названий моделей, большинство из которых отражает решение некоторой конкретной задачи. Ниже приведена классификация и дана характеристика наиболее общих видов моделей.

Содержание

Требования к моделям

Моделирование всегда предполагает принятие допущений той или иной степени важности. При этом должны удовлетворяться следующие требования к моделям:

Выбор модели и обеспечение точности моделирования считается одной из самых важных задач моделирования.

Точность моделей

Погрешности моделирования вызываются как объективными причинами, связанными с упрощением реальных систем, так и субъективными, обусловленными недостатком знаний и навыков, особенностями характера того или иного человека. Погрешности можно предотвратить, компенсировать или учесть. И всегда обязательна оценка правильности получаемых результатов. В технике быструю оценку точности модели часто проводят следующими способами:

Известно, что посредством грубых измерений, использования контрольно-измерительных приборов с низкой точностью или приближенных исходных данных невозможно получить точные результаты. С другой стороны, бессмысленно вести, например, расчет с точностью до грамма, если результат потом нужно округлять (скажем, указывать в формуляре) с точностью до ста грамм, или же определять среднюю величину точнее составляющих её значений, и т. д. Поэтому важно помнить о следующем:

Основные виды моделей

По способу отображения действительности различают три основных вида моделей — эвристические, натурные и математические.

Эвристические модели

Эвристические модели, как правило, представляют собой образы, рисуемые в воображении человека. Их описание ведется словами естественного языка (например, вербальная информационная модель) и, обычно, неоднозначно и субъективно. Эти модели неформализуемы, то есть не описываются формально-логическими и математическими выражениями, хотя и рождаются на основе представления реальных процессов и явлений.

Эвристическое моделирование — основное средство вырваться за рамки обыденного и устоявшегося. Но способность к такому моделированию зависит, прежде всего, от богатства фантазии человека, его опыта и эрудиции. Эвристические модели используют на начальных этапах проектирования или других видов деятельности, когда сведения о разрабатываемой системе ещё скудны. На последующих этапах проектирования эти модели заменяют на более конкретные и точные.

Натурные модели

Отличительной чертой этих моделей является их подобие реальным системам (они материальны), а отличие состоит в размерах, числе и материале элементов и т. п. По принадлежности к предметной области модели подразделяют на следующие:

Физическое моделирование — основа наших знаний и средство проверки наших гипотез и результатов расчетов. Физическая модель позволяет охватить явление или процесс во всём их многообразии, наиболее адекватна и точна, но достаточно дорога, трудоемка и менее универсальна. В том или ином виде с физическими моделями работают на всех этапах проектирования;

Математические модели

Математические модели — формализуемые, то есть представляют собой совокупность взаимосвязанных математических и формально-логических выражений, как правило, отображающих реальные процессы и явления (физические, психические, социальные и т. д.). По форме представления бывают:

Построение математических моделей возможно следующими способами (более подробно — см. Математическая модель):

Математические модели более универсальны и дешевы, позволяют поставить «чистый» эксперимент (то есть в пределах точности модели исследовать влияние какого-то отдельного параметра при постоянстве других), прогнозировать развитие явления или процесса, отыскать способы управления ими. Математические модели — основа построения компьютерных моделей и применения вычислительной техники.

Результаты математического моделирования нуждаются в обязательном сопоставлении с данными физического моделирования — с целью проверки получаемых данных и для уточнения самой модели. С другой стороны, любая формула — это разновидность модели и, следовательно, не является абсолютной истиной, а всего лишь этап на пути её познания.

Промежуточные виды моделей

К промежуточным видам моделей можно отнести:

Существует и другие виды «пограничных» моделей, например, экономико-математическая и т. д.

Выбор типа модели зависит от объема и характера исходной информации о рассматриваемом устройстве и возможностей инженера, исследователя. По возрастанию степени соответствия реальности модели можно расположить в следующий ряд: эвристические (образные) — математические — натурные (экспериментальные).

Уровни моделей

Количество параметров, характеризующих поведение не только реальной системы, но и её модели, очень велико. Для упрощения процесса изучения реальных систем выделяют четыре уровня их моделей, различающиеся количеством и степенью важности учитываемых свойств и параметров. Это — функциональная, принципиальная, структурная и параметрическая модели.

Функциональная модель

Функциональная модель предназначена для изучения особенностей работы (функционирования) системы и её назначения во взаимосвязи с внутренними и внешними элементами.

Функция — самая существенная характеристика любой системы, отражает её предназначение, то, ради чего она была создана. Подобные модели оперируют, прежде всего, с функциональными параметрами. Графическим представлением этих моделей служат блок-схемы. Они отображают порядок действий, направленных на достижение заданных целей (т. н. ‘функциональная схема’). Функциональной моделью является абстрактная модель.

Модель принципа действия

Модель принципа действия (принципиальная модель, концептуальная модель) характеризует самые существенные (принципиальные) связи и свойства реальной системы. Это — основополагающие физические, биологические, химические, социальные и т. п. явления, обеспечивающие функционирование системы, или любые другие принципиальные положения, на которых базируется планируемая деятельность или исследуемый процесс. Стремятся к тому, чтобы количество учитываемых свойств и характеризующих их параметров было небольшим (оставляют наиболее важные), а обозримость модели — максимальной, так чтобы трудоемкость работы с моделью не отвлекала внимание от сущности исследуемых явлений. Как правило, описывающие подобные модели параметры — функциональные, а также физические характеристики процессов и явлений. Принципиальные исходные положения (методы, способы, направления и т. д.) лежат в основе любой деятельности или работы.

Так, принцип действия технической системы — это последовательность выполнения определенных действий, базирующихся на определенных физических явлениях (эффектах), которые обеспечивают требуемое функционирование этой системы. Примеры моделей принципа действия: фундаментальные и прикладные науки (например, принцип построения модели, исходные принципы решения задачи), общественная жизнь (например, принципы отбора кандидатов, оказания помощи), экономика (например, принципы налогообложения, исчисления прибыли), культура (например, художественные принципы).

Работа с моделями принципа действия позволяет определить перспективные направления разработки (например, механика или электротехника) и требования к возможным материалам (твердые или жидкие, металлические или неметаллические, магнитные или немагнитные и т. д.).

Правильный выбор принципиальных основ функционирования предопределяет жизнеспособность и эффективность разрабатываемого решения. Так, сколько бы ни совершенствовали конструкцию самолета с винтомоторным двигателем, он никогда не разовьет сверхзвуковую скорость, не говоря уже о полетах на больших высотах. Только использование другого физического принципа, например, реактивного движения и созданного на его основе реактивного двигателя, позволит преодолеть звуковой барьер.

Например, для технических моделей эти схемы отражают процесс преобразования вещества, как материальной основы устройства, посредством определенных энергетических воздействий с целью реализации потребных функций (функционально-физическая схема). На схеме виды и направления воздействия, например, изображаются стрелками, а объекты воздействия — прямоугольниками.

Структурная модель

Четкого определения структурной модели не существует. Так, под структурной моделью устройства могут подразумевать:

Под структурной моделью процесса обычно подразумевают характеризующую его последовательность и состав стадий и этапов работы, совокупность процедур и привлекаемых технических средств, взаимодействие участников процесса.

Например, — это могут быть упрощенное изображение звеньев механизма в виде стержней, плоских фигур (механика), прямоугольники с линиями со стрелками (теория автоматического управления, блок-схемы алгоритмов), план литературного произведения или законопроекта и т. д. Степень упрощения зависит от полноты исходных данных об исследуемом устройстве и потребной точности результатов. На практике виды структурных схем могут варьироваться от несложных небольших схем (минимальное число частей, простота форм их поверхностей) до близких к чертежу изображений (высокая степень подробности описания, сложность используемых форм поверхностей).

Возможно изображение структурной схемы в масштабе. Такую модель относят к структурно-параметрической. Её примером служит кинематическая схема механизма, на которой размеры упрощенно изображенных звеньев (длины линий-стержней, радиусы колес-окружностей и т. д.) нанесены в масштабе, что позволяет дать численную оценку некоторым исследуемым характеристикам.

Для повышения полноты восприятия на структурных схемах в символьном (буквенном, условными знаками) виде могут указывать параметры, характеризующие свойства отображаемых систем. Исследование таких схем позволяет установить соотношения (функциональные, геометрические и т. п.) между этими параметрами, то есть представить их взаимосвязь в виде равенств f (x₁, х₂, …) = 0, неравенств f (x₁, х₂, …) > 0 и в иных выражениях.

Параметрическая модель

Под параметрической моделью понимается математическая модель, позволяющая установить количественную связь между функциональными и вспомогательными параметрами системы. Графической интерпретацией такой модели в технике служит чертеж устройства или его частей с указанием численных значений параметров.

Классификация моделей

По целям исследований

В зависимости от целей исследования выделяют следующие модели:

По особенностям представления

С целью подчеркнуть отличительную особенность модели их подразделяют на простые и сложные, однородные и неоднородные, открытые и закрытые, статические и динамические, вероятностные и детерминированные и т. д. Стоит отметить, что когда говорят, например, о техническом устройстве как простом или сложном, закрытом или открытом и т. п., в действительности подразумевают не само устройство, а возможный вид его модели, таким образом подчеркивая особенность состава или условий работы.

Знание этих особенностей облегчает процесс моделирования, так как позволяет выбрать вид модели, наилучшим образом соответствующей заданным условиям. Этот выбор основывается на выделении в системе существенных и отбрасывании второстепенных факторов и должен подтверждаться исследованиями или предшествующим опытом. Наиболее часто в процессе моделирования ориентируются на создание простой модели, что позволяет сэкономить время и средства на её разработку. Однако повышение точности модели, как правило, связано с ростом её сложности, так как необходимо учитывать большое число факторов и связей. Разумное сочетание простоты и потребной точности и указывает на предпочтительный вид модели.

Источник

Значение слова «модель»

1. Образцовый экземпляр какого-л. изделия, а также образец для изготовления чего-л. Выставка моделей женского платья. □ На жене шитье по самой новейшей парижской модели. Куприн, Мученик моды.

3. Тип, марка, образец конструкции. Новая модель автомобиля.

4. Воспроизведение или схема чего-л., обычно в уменьшенном виде. У левой стены находился огромный бассейн, в котором плавали модели военных судов. М. Горький, Мои интервью. Перед ними стояли в моделях и в натуральном виде сотни замечательных машин и приборов. Закруткин, Плавучая станица. Баженов усердно делает модели с лучших зданий Рима. М. А. Ильин, В. И. Баженов.

5. Спец. Вспомогательный объект (или система), заменяющий изучаемый объект, представленный в наиболее общем виде. Как мы уже говорили, в современном научном познании все большую роль приобретают информационные модели, которые, будучи как бы «информационными слепками» оригинала, могут замещать последний на определенных стадиях исследования. В. Парин, Б. Бирюков и др., Проблемы кибернетики. Всем известная теперь модель атома по Резерфорду есть не что иное, как некая солнечная система, состоящая из ядра — солнца и электронов — планет. Л. Гумилевский, Вернадский.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Модель есть абстрактное представление реальности в какой-либо форме (например, в математической, физической, символической, графической или дескриптивной), предназначенное для представления определённых аспектов этой реальности и позволяющее получить ответы на изучаемые вопросы:80.

МОДЕ’ЛЬ [дэ], и, ж. [фр. modèle]. 1. Образец, образцовый экземпляр какого-н. изделия (спец.). М. товара. М. платья. 2. Воспроизведенный, обычно в уменьшенном виде, образец какого-и. сооружения (тех.). М. машины. 3. Тип, марка, образец конструкции. Автомобиль новой модели. 4. Натурщик, натурщица, какой-н. предмет, служащий материалом для художественного воспроизведения, изображения (искус.). 5. В литейном деле — образец для изготовления формы, в которой должен отливаться какой-н. предмет (тех.). 6. Геометрический чертеж, схема для пояснения какого-н. физического явления или процесса (науч.). М. строения атома. 7. перен. О ком-чем-н., служащем примером, образцом каких-нибудь действий. Это — м. для подражания. ◊

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

моде́ль

1. образец изделия, по которому осуществляется серийное воспроизводство ◆ Серийный образец утратил имевшиеся на опытной модели ребра радиатора ствола и дульный компенсатор «МР5 «Хенклер унд Кох»: бессмертный лидер», 2004 г. // «Солдат удачи» (цитата из НКРЯ)

2. тип, марка, образец конструкции ◆ Каждый, кто интересуется новой моделью, может не только поглазеть на машину, но и испытать её в ходе тест-драйва. «Официальные дилеры», 2002 г. // «Автопилот» (цитата из НКРЯ)

3. изделие из твердого материала, служащее образцом, с которого снимается форма для отливки или для воспроизведения в другом материале ◆ Между множеством прекрасных моделей в мастерской г. Витали заметили мы превосходный барельеф: «Исаакий, уносимый на небо тремя ангелами», над которым мы застали художника; бюст покойной великой княжны Александры Николаевны, так рано похищенной смертию; известную его богородицу с ребёнком-Христом… Тургенев, «Современные заметки»

4. воспроизведение или схема какого-либо материального объекта, обычно в уменьшенном виде ◆ Более ответственные, со сложным профилем, обрабатываются на моделях, специально отлитых из баббита — металлического сплава на основе олова или свинца, с низкой температурой плавления. Константин Скворцов, «От кубка до рыцарского шлема», 2004 г. // «Народное творчество» (цитата из НКРЯ)

5. тот, кто позирует перед фотографом или художником, служит образцом для изображения, воспроизведения; натурщик, натурщица ◆ Многие из синьор служили моделями для живописцев. Гоголь, «Рим»

6. тот, кто демонстрирует на подиуме образцы одежды ◆ По подиуму дефилирует модель в новом платье от Джанни Версаче.

7. идея или схема, объясняющая или описывающая какой-либо объект, природное или общественное явление ◆ Предложена теоретическая модель, описывающая испускание частичных дислокаций границами зёрен в нанокристаллических металлах при пластической деформации. «Эмиссия частичных дислокаций границами зерен в нанокристаллических металлах», 2004 г. // «Физика твердого тела» (цитата из НКРЯ)

8. одуш. разг. женщина, чья внешность соответствует некоторым стандартам

Источник

Понятия модели и моделирования

Математические модели в науке как средство работы с информацией

Невозможно представить себе современную науку без широкого применения математического моделирования, суть которого состоит в замене исходного объекта его образом – математической моделью и дальнейшем изучении модели с помощью реализуемых на компьютерах вычислительно-логических алгоритмов. Этот метод сочетает в себе достоинства, как теории, так и эксперимента, поскольку работа не с самим объектом (явлением, процессом), а с его моделью дает возможность относительно быстро и без существенных затрат исследовать его свойства и поведение в различных ситуациях. В то же время вычислительные эксперименты с моделями объектов позволяют, опираясь на мощь современных вычислительных методов и технических средств информатики, подробно и глубоко изучать объекты в достаточной полноте, недоступной чисто теоретическим подходам.

Вышесказанное является актуальным в условиях постоянного роста требований к эффективности устройств, применяемых в системах передачи и обработки информации, к сокращению сроков исследования и разработки новых телекоммуникационных систем и сетей.

Моделирование можно рассматривать как замещение исследуемого объекта (оригинала) его условным образом, описанием или другим объектом, именуемым моделью и обеспечивающим близкое к оригиналу поведение в рамках некоторых допущений и приемлемых погрешностей. Моделирование обычно выполняется с целью познания свойств оригинала путем исследования его модели, а не самого объекта. Разумеется, моделирование оправдано в том случае когда оно проще создания самого оригинала или когда последний по каким-то причинам лучше вообще не создавать.

М. строится для достижения определенной цели, однако для одного и того же объ­екта можно построить, преследуя одну и ту же цель, разные модели. Поэтому можно считать, что М. некоторого объекта А (оригинала, прототипа) – это объект В, в каком-то отноше­нии подобный (аналогичный) оригиналу А, но отличающийся от него, вы­бранный или по­строенный, по крайней мере, для одной из следующих целей:

1) замена оригинала А моделью B в некотором реальном или воображаемом дейст­вии, ис­ходя из того, что В более удобна для осуществления этого действия в данных условиях (т.н. называемая модель-заместитель);

2) создание наглядного представления об объекте А (реально существующем или вообра­жаемом) с помощью объекта В (т.н. называемая модель-представление);

3) истолкование (интерпретация) объекта А в виде модели В (т.н. называемая мо­дель-ин­терпретация);

4) исследование (изучение) объекта А посредством изучения объекта В (т.н. назы­ваемая исследовательская модель).

Пример.1. В курсе математики представлены все перечис­ленные виды мо­делей. Так, уравне­ние, со­ставленное по условию текстовой задачи, вы­сту­пает как модель-заместитель исходной задачи; чер­теж некоторого геометрического объекта, построенный для доказательства утверждения, в кото­ром идет речь в этом утверждении, яв­ляется моде­лью-представлением рассматриваемого объекта; урав­нение (x–a) 2 + (y – b) 2 = R 2 является моделью-интерпретацией окружности.

М. обычно обладает не одним каким-либо признаком, соответствующим одной из указанных целей, а несколькими, и поэтому она пригодна, как правило, и для других целей. Например, модель-заместитель может использоваться и как модель-представ­ление, и как мо­дель-интерпретация, и как исследовательская модель. Так, модель-ин­терпретация окружно­сти вполне пригодна для исследования свойств окружности, а, значит, она является и моде­лью исследовательской.

Пример 2. В медицине многие лекарственные препараты, разрабатывае­мые для лечения людей, первоначально испытывают на животных, которые в этом случае и выступают в качестве модели че­ловека; моделью некоторой местности может служить географическая карта, пользуясь которой, мы получаем нужную нам информацию об этой местности; моделью прямолиней­ного равномерного движения служит уравнение s = v₀ +vt, исследование ко­торого дает воз­можность устанавливать ос­новные закономерности данного вида движения; моделью неко­торого предмета, явления, процесса или ситуации (как реальных, так и «вирту­альных») могут служить компьютерные программы, пре­доставляющие в распоряжение ис­следователя прак­тически неограниченные возможности для их изу­чения и прогнозирования развития; и т.п.

М. всегда является лишь ото­бражением оригинала, и она в каком-либо отношении должна быть не только удобна для изучения свойств исследуемого объекта, но и по­зволяет перенести по­лученные при этом знания на исходный объект. Например, когда в начальных школе учитель намеревается более наглядно продемонстрировать способ сложения нату­ральных чисел, то он использует для этого различные модели этих чи­сел: реальные пред­меты или их изображения, абак, русские счеты, и др. Многие дет­ские игрушки, пред­ставляющие собой модели реальных объектов (автомобилей, по­ездов, животных и т.п.), позволяют ребенку познавать определенные свойства окру­жающих его предметов.

М., полностью воспроизводящая оригинал, перестает быть моделью.

Существует ряд общих требований к моделям:

1. Адекватность – достаточно точное отображение свойств объекта;

2. Полнота – предоставление получателю всей необходимой информации об объекте;

3. Гибкость – возможность воспроизведения различных ситуаций во всем диапазоне изменения условий и параметров;

4. Трудоемкость разработки должна быть приемлемой для имеющегося времени и программных средств.

Моделирование – это процесс построения модели объекта и исследования его свойств путем исследования модели.

Таким образом, моделирование предполагает 2 основных этапа:

1. Разработка модели;

2. Исследование модели и получение выводов.

При этом на каждом из этапов решаются разные задачи и используются отличающиеся по сути методы и средства.

Метод моделирования во многих науках является средством, позволяющим ус­та­навли­вать более глубокие и сложные взаимосвязи между теорией и опытом и способ­ным заменить эксперимент.

Целый ряд исследований вообще невозможен без моде­лирования, по­тому, что:

а) эксперименты могут проводиться лишь на ныне существующих объектах, т.к. невоз­можно распространить эксперимент в область прошлого;

б) вмешательство в некоторые системы иногда имеет такой характер, что невоз­можно ус­тановить причины появившихся изменений (вследствие вмешательства или по другим при­чинам);

в) некоторые теоретически возможные эксперименты неосуществимы вследствие низ­кого уровня развития экспериментальной техники или ее высокой стоимости;

г) большую группу экспериментов, связанных с человеком, сле­дует отклонить по мо­рально-этическим соображениям.

Однако М. находит широкое применение не только из-за того, что может за­менить эксперимент.

Оно имеет большое самостоятельное значение и свои преимущества:

1. С помощью метода моделирования на одном комплексе данных можно разрабо­тать целый ряд различных моделей, по-разному интерпретировать исследуемое явле­ние, и вы­брать наи­более плодотворную из них для теоретического истолкования.

2. В процессе построения модели можно сделать различные дополнения к иссле­дуемой ги­потезе и получить ее упрощение.

3. В случае сложных моделей можно применять компьютерную технику.

4. Существует возможность проведения модельных экспериментов. И др.

На практике применяют различные методы моделирования. В зависимости от способа реализации, все модели можно разделить на два больших класса: физические и математические.

Математическое моделирование принято рассматривать как средство исследования процессов или явлений с помощью их математических моделей.

Под физическим моделированием понимается исследование объектов и явлений на физических моделях, когда изучаемый процесс воспроизводят с сохранением его физической природы или используют другое физическое явление, аналогичное изучаемому. При этом физические модели предполагают, как правило, реальное воплощение тех физических свойств оригинала, которые являются существенными в конкретной ситуации. Например, при проектировании нового самолета создается его макет, обладающий теми же аэродинамическими свойствами; при планировании застройки архитекторы изготавливают макет, отражающий пространственное расположение ее элементов. В связи с этим физическое моделирование называют также макетированием.

Очевидно, действительная польза от моделирования может быть получена только при соблюдении двух условий:

1. Модель обеспечивает корректное (адекватное) отображение свойств оригинала, существенных с точки зрения исследуемой операции;

2. Модель позволяет устранить перечисленные выше проблемы, присущие проведению исследований на реальных объектах

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ – приближенное описание ка­кого-либо явле­ния внешнего мира, выраженное с помощью математической сим­волики. Ма­тематиче­ские модели описываются с помощью средств самой математики: языка, понятий, отно­шений, теорий. В отличие от есте­ственнонауч­ных и гуманитарных дисциплин М.м. обычно не требует создания ма­териали­зованных объектов. Кроме то­го, если все дру­гие науки изу­чают модели, то ма­тематика изучает «модели моделей». Потому ее мате­риал в наилуч­шей степени соответствует задаче овладения методом моделиро­вания.

Примером М.м. достаточно сложно­го оригинала служит система уравне­ний (и не­равенств) в самом широком понимании. Система может содержать обыкновен­ные дифферен­циальные уравнения, уравнения в частных производных, интегральные уравнения, алгебраи­ческие и трансцендентные уравнения (и неравенства), набор ве­роятностно-статистических данных и т.д. К математическим моделям относят и про­граммы, составленные для ком­пьютеров, которые моделирую (отражают) оп­ределен­ные процессы, описанные средст­вами математики, положенными в основу ал­горит­мов.

В 80-х годах XX века появляются оригинальные работы в области глобального модели­рования в Советском Союзе. Группой ученых под руководством академика Н.Н. Моисеева в Вычисли­тельном Центре АН СССР была сделана попытка проанализировать математиче­скими мето­дами структуру международной конфликтной ситуа­ции. Основной вывод, кото­рый сле­довал из анализа составлен­ной модели, состоял в следующем. Несмотря на сложную зависи­мость целевой функции, общей для всех партнеров (функции риска ядерной войны), в дейст­виях участников конфликта, в такой сверх­сложной и сверхопасной ситуации, какой является гонка ядерных воо­ружений, существует взаимо­выгодный и эффективный компромисс.

МЕТОД МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ сводит исследование внешнего мира к мате­ма­тическим задачам.

Процесс математического моделирования состоит из четырех эта­пов:

1) формализации, т. е. перехода от реальной практической задачи (исследуемой си­туа­ции) к по­строению аде­к­ватной математической модели и формулировки на ее ос­нове абст­рактной математической задачи;

2) решения задачи путем преоб­разования модели (проведение математического иссле­дования), т.е. получение в результате анализа и исследования модели выходных данных (теоретических сведений);

3) интерпретации полученного результата, когда решение формальной математи­че­ской задачи исследуется на предмет его соответствия с исходной ситуацией, истол­ковыва­ется в терминах исходной ситуации и применяется к ней;

4) модернизации модели, т.е. построение новой более совершенной модели в связи с на­коплением данных об изучаемом объекте или процессе.

Пример 4. Разработка модели Сол­нечной системы. Наблюдения звездного неба, начавшиеся еще в глубокой древности, при­вели к тому, что из всего многообразия небесных светил были выде­лены планеты, которые и стали объектом изучения. Следующим ша­гом явилось изучение закономер­ностей их дви­жений, т.е. построение моделей и получение конкретных резуль­татов. Модели Солнеч­ной системы в процессе своего развития прошли через ряд усовершенствований по мере накоп­ления экспе­риментальных данных и развития науки. Первой была модель Птолемея, создан­ная во II веке нашей эры, исходила из положения, что планеты и Солнце совершают движе­ния вокруг Земли (т.н. геоцентриче­ская модель).

В XVI веке появилась модель Н. Коперника, принципи­ально отличающаяся от предыдущей, пола­гающая, что планеты вращаются вокруг Солнца по окружности (т.н. гелиоцен­три­ческая модель). Затем появи­лась модели И. Кеплера (начало XVII века), И. Ньютона (вторая поло­вина XVII века), описывающие движения пла­нет на ма­тематическом языке. Модель Ньютона, осно­ванная на законе всемирного тяготения, вполне удовлетворительно описывала движение известных планет и давала возможность вы­чис­лять их положение на небо­своде.

Но вот к 40-м годам XIX в. не­которые результаты этой мо­дели стали тоже не согласовываться с экспе­риментальными данными: наблюдаемое движе­ние Урана уклонялось от теоретически вычисляемого движения. Французский ученый-ас­троном У. Леверье расширил систему наблюдаемых планет новой гипотетической плане­той (он на­звал ее Нептуном) и, пользуясь новой математической моделью, определил все ос­нов­ные па­раметры этой планеты. В указанное время и на предсказанном им месте в 1846 году астро­номы убедились в реальном существовании еще одной планеты Солнечной сис­темы. По­добные вычисле­ния, сделанные П. Лоуэлом, при­вели в 1930 году к открытию де­вятой пла­неты, получившей название Плутон.

В ходе многовекового исторического развития математики сконст­руированы осо­бые мо­дели количественных отношений и пространственных форм ок­ружаю­щего мира. Это такие математические понятия, как число, функция, уравнение, гео­метриче­ская фигура и др. Хотя математическая модель и создается человеческим разумом, в даль­нейшем она во многих случаях становится предметом объективного изучения. Познавая ее свойства, мы тем самым познаем и свойства отраженной моделью реаль­но­стей, т.е. абст­рактные математические открытия обнаруживают ранее неизвестные свойства окружающего мира.

Например, представле­ние, что числа бывают только, скажем, до миллиарда (а дальше чисел нет!) прямым наблюдением вряд ли может быть опро­вергнуто. Только создание мате­матиками древности такого понятия нату­рального числа (такой модели), при ко­тором нату­ральных чисел оказывалось беско­нечно много, позволяет это сделать. С помощью модели геометрии Лобачевского че­ловечество пришло к пониманию искрив­ленности пространства, абстрактные функ­циональные зависимости дают возможность пред­сказывать развитие тех или иных процессов, модели геометрических тел позволяют на прак­тике определять количе­ст­венные характеристики окружающих нас предметов и т.д.

Для исследования существующих и построения новых моделей в математике раз­рабо­таны специальные методы. Среди них методы теории графов, теории вероятно­стей и математической статистики, математической логики и комбинаторики, ак­сио­матический метод, методы иссле­дования элементарных функций, решения уравнений, доказательства утверждений, построения геометрических фигур, измерения величин и т.д. Так, идеи метода моделирования находят свое примене­ние при решении тексто­вых задач: во-первых, само понятие текстовой задачи можно ввести, пользуясь поня­тием «модель», во-вторых, понятия мо­дели позволяет строго определить понятия «метода решения» и «способа решения» тексто­вой задачи.

В математике разработаны и особые методики использования на практике матема­тиче­ских моде­лей, например, приемы решения задач с помощью уравнений и систем уравнений, изучение различных явлений и процессов с помощью исследования соот­ветствующих функ­ций, графов, геометрических фигур и т.д.

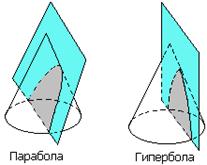
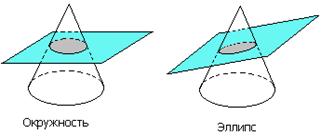
Пример 5. Общеизвестно, что, разрезая конус плоскостями, не проходящими через его вершину, мы полу­чаем в сечении различные кривые: окружности, эллипсы, параболы, гиперболы (рис. 4.7). Их называют коническими сече­ниями. Еще древнегреческие ученые начали зани­маться изучением этих кривых, т.к. они встречаются в различ­ных явлениях природы и в че­ловече­ской деятельности (в астро­номии, в во­енном деле, в физики и т.п.). Однако лишь, ко­гда поя­вились уравнения конических сечений, полу­ченные методом координат, изучение этих кри­вых значительно продвинулось вперед, и были ре­шены многие задачи, связанные с ними. Так, И. Кеплер (1609 г.) открыл из наблюдений, а И. Ньютон (1687 г.) теоретически обосно­вал, что планеты и кометы Солнечной сис­темы движутся по этим кривым.

З.м. понятия «число». Понятие числа явля­ется одним из важнейших в математике и центральным понятием курса математики в на­чальной. Появившись в простейшем виде еще в первобытном об­ществе из потребностей счета, понятие числа совершенст­вова­лось на протяжении всего последующего развития человеческой цивилизации. В вузе сту­денты, в силу выбранной профессии, изучают большинство известных число­вых множеств, и они знают, что развитие понятия числа происходило под влиянием двух факторов: прак­тиче­ской деятельности человека и внутренних потребностей ма­тематики. В процессе обучения у них формируется представление о том, что бывают порядковые числа, ко­личественные числа, числа как меры величин и числа как ком­понент вычислений.

Системы счисления и нумерации – это способы знаково-сим­воличе­ского модели­рования натуральных чисел. Например, любое натуральное число s в десятич­ной сис­теме счисления можно представить в виде:

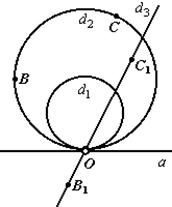
Геометрия Лобачевского, не получившая признания при жизни ее автора, стала из­вест­ной только после того, как появилась ее первая модель.

Можно показать, что на этой модели выполняются все аксиомы геометрии Евклида кроме ак­сиомы IV о па­раллельных. Вместо нее выполняется аксиома Лобачевского: «Через точку вне прямой проходит более одной прямой, не пересекающей данную». На рис 9а через точку O проходят три «прямые» d₁, d₂ и d₃, параллельные «прямой» a.

Наличие моделей доказывает, что сис­тема ак­сиом Лобачевского является непро­тиворечивой.

Построение моделей геометрий Евклида и Лобачевского позволило решить про­блему 2000-летней дав­ности: можно ли доказать аксиому о параллельных, т.е. вы­вести ее из дру­гих аксиом? Те­перь ясно, что нельзя, потому что эта аксиома не зави­сит от остальных ак­сиом. Независи­мость вытекает из того факта, что после замены аксио­мы параллельности Евклида на ак­сиому параллельности Лобачевского мы вновь получаем непротиворечивую си­стему аксиом.

Открытие неевклидовой геометрии показывает, что появление новых математиче­ских мо­делей нередко означает не только принципиальный поворот в развитии самой математики, но и меняет существующие знания об окружающем нас мире.

МОДЕЛИ В ОБУЧЕНИИ. Модели помимо всего прочего являются тем учебным средством, без кото­рого невоз­можно полно­цен­ное обучение. На уроках математике в начальной школе находят применение как материальные, так и идеальные модели. К ним относятся, например, наглядные пособия, которые воспроизводят реальные и идеальные объекты, передают их структуру, существенные свойства, связи и от­ноше­ния, допуская при этом уменьшение или увеличение раз­мера, схематическое изобра­же­ние. По способу предъявления учащимся такие модели делятся на демонстрацион­ные и раз­даточные (индивидуальные).

Источник