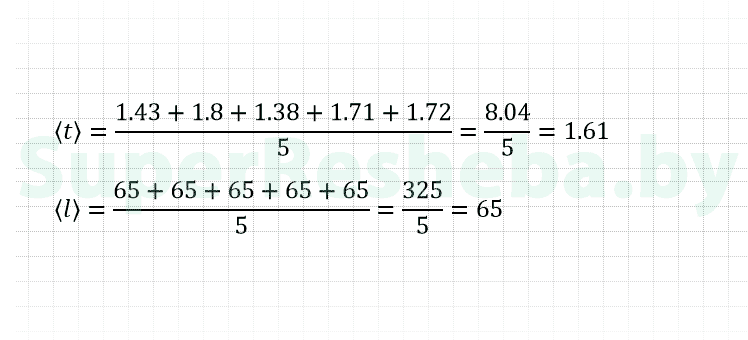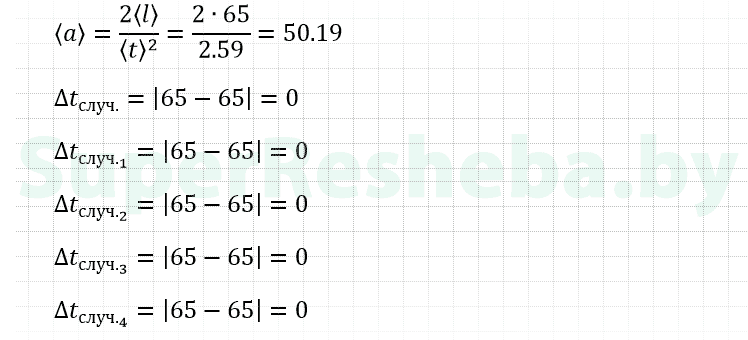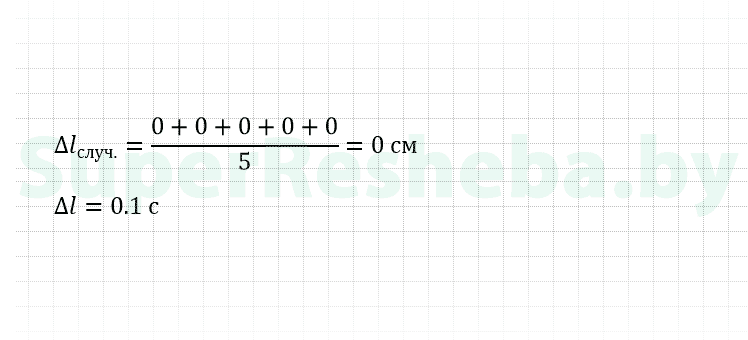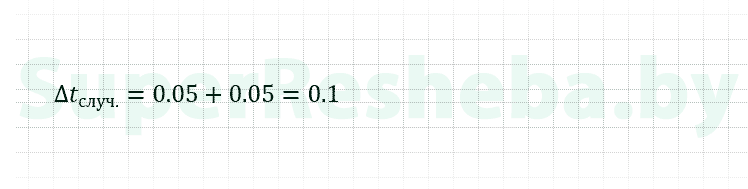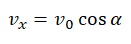Что представляет модуль перемещения при данном движении шарика как направлен вектор шарика
6. Вычислите и занесите в таблицу среднее значение ускорения шарика по формуле.
7. Рассчитайте и занесите в таблицу значение абсолютной погрешности Δl.
8. Вычислите максимальное значение абсолютной случайной погрешности измерения промежутка времени t.
9. Определите абсолютную систематическую погрешность промежутка времени t.
10. Вычислите значение абсолютной погрешности прямого измерения промежутка времени t.
11. Вычислите значения относительной погрешности измерения длины и промежутка времени.
| l | t | a | Δl | Δt | ε | ε | |
| 1 | 65 | 1,43 | — | 0,1 | 0,48 | 0,15 | 29,81 |
| 2 | 65 | 1,8 | — | — | — | — | — |
| 3 | 65 | 1,38 | — | — | — | — | — |
| 4 | 65 | 1,71 | — | — | — | — | — |
| 5 | 65 | 1,72 | — | — | — | — | — |
| Ср. | 65 | 1,61 | 50,19 | — | — | — | — |
Ответьте на контрольные вопросы
1. Что представляет модуль перемещения при данном движении шарика? как направлен вектор перемещения?
Представляет вектор, который соединяет две точки траектории движения — начальную и конечную. Вектор в данном случае это желоб.
2. Будут ли равными средние скорости шарика при его движении на первой и второй половинах пути? Почему?
Средние скорости будут различны, т. к. во время движения на шарик действую силы тяготения и трения, которые способны замедлять его.
Выводы: научился вычислять ускорение скатывающегося шарика и погрешности измерений времени движения шарика по желобу.
Лаб. 2
| $l$ | $t$ | $a$ | $Δl$ | $Δt$ | $ε$ | $ε$ | |
| $1$ | $65$ | $1,43$ | $-$ | $0,1$ | $0,48$ | $0,15$ | $29,81$ |
| $2$ | $65$ | $1,8$ | $-$ | $-$ | $-$ | $-$ | $-$ |
| $3$ | $65$ | $1,38$ | $-$ | $-$ | $-$ | $-$ | $-$ |
| $4$ | $65$ | $1,71$ | $-$ | $-$ | $-$ | $-$ | $-$ |
| $5$ | $65$ | $1,72$ | $-$ | $-$ | $-$ | $-$ | $-$ |
| Ср. | $65$ | $1,61$ | $50,19$ | $-$ | $-$ | $-$ | $-$ |
1. Что представляет модуль перемещения при данном движении шарика? Как направлен вектор перемещения?
Представляет вектор, который соединяет две точки траектории движения — начальную и конечную. Вектор в данном случае это желоб.
2. Будут ли равными средние скорости шарика при его движении на первой и второй половинах пути? Почему?
Средние скорости будут различны, т. к. во время движения на шарик действую силы тяготения и трения, которые способны замедлять его.
Выводы: научился вычислять ускорение скатывающегося шарика и погрешности измерений времени движения шарика по желобу.
Что представляет модуль перемещения
модуль S его перемещения, модуль средней скорости, а также среднепутевую скорость
Катер движется по озеру с постоянной по модулю скоростью 18 км/ч. Сначала в течении 1 минуты 40.
Модуль перемещения
Помогите разобраться с задачей. Качество не ахти, но, пожалуйста, помогите, последняя задача.
найти модуль вектора перемещения
Радиус- вектор материальной точки изменяется по закону : r(t) =t^2*(6i+8j) (cм) Найлидитель модуль.
Определите путь и модуль вектора перемещения
Помогите решить 2 задачи 1. Тело совершает пол оборота(вокруг окружности) определите путь и модуль.
Скажите пожалуйста чему равна
дэльта L отсчета?
Добавлено через 34 минуты
пожалуйста ответьте хоть кто-нибудь прошу пожалуйстааа
А можете еще пожалуйста ответить
1)Какие положения шарика(в верхней или нижней части снимка на рисунки 1) целесообразнее брать для определения модуля ускорения.Почему?
2)В каком соотношение будут модули перемещений шарика за равные последовательные промежутки времени?
Добавлено через 18 секунд
щас я картинку скину
Найти модуль перемещения тела к концу третьей секунды от начала отсчета времени
Уравнение движения тела имеют следующий вид : x=11-4t ; y=3t-1.(все в метрах)Найти модуль.
Модуль cisco VIC-2FXO что из себя представляет и как его настроить
Друзья, помогите понять что из себя представляет модуль cisco VIC-2FXO. Как его настроить? Для чего.
Определить путь и модуль перемещения вертолета
3. Вертолет, пролетев в горизонтальном направлении по прямой 4 км, вернул под углом 90 градусов и.
С нами ты учишься лучше
Лабораторная 2: Определение ускорения при равноускоренном движении тела
5. Найдите и занесите в таблицу средние значения l> и t>.
6. Вычислите и занесите в таблицу среднее значение ускорения шарика по формуле.
7. Рассчитайте и занесите в таблицу значение абсолютной погрешности Δ l.
8. Вычислите максимальное значение абсолютной случайной погрешности измерения промежутка времени t.
9. Определите абсолютную систематическую погрешность промежутка времени t.
10. Вычислите значение абсолютной погрешности прямого измерения промежутка времени t.
11. Вычислите значения относительной погрешности измерения длины и промежутка времени.
| l | t | a | Δ l | Δ t | ε | ε | |
| 1 | 65 | 1,43 | — | 0,1 | 0,48 | 0,15 | 29,81 |
| 2 | 65 | 1,8 | — | — | — | — | — |
| 3 | 65 | 1,38 | — | — | — | — | — |
| 4 | 65 | 1,71 | — | — | — | — | — |
| 5 | 65 | 1,72 | — | — | — | — | — |
| Ср. | 65 | 1,61 | 50,19 | — | — | — | — |
Ответьте на контрольные вопросы
1. Что представляет модуль перемещения при данном движении шарика? как направлен вектор перемещения?
Представляет вектор, который соединяет две точки траектории движения — начальную и конечную. Вектор в данном случае это желоб.
2. Будут ли равными средние скорости шарика при его движении на первой и второй половинах пути? Почему?
Средние скорости будут различны, т. к. во время движения на шарик действую силы тяготения и трения, которые способны замедлять его.
Выводы: научился вычислять ускорение скатывающегося шарика и погрешности измерений времени движения шарика по желобу.
Движение тела, брошенного под углом к горизонту
теория по физике 🧲 кинематика
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты! График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
Уравнение координаты x:
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Алгоритм решения
Решение
Запишем исходные данные:
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Потенциальная энергия шарика в точке А равна:
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
Перед ударом кинетическая энергия шарика равна:
Согласно закону сохранения энергии:
E p A = E p B + E k B
Отсюда высота H равна:
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
pазбирался: Алиса Никитина | обсудить разбор | оценить
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить