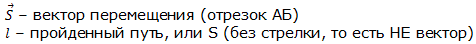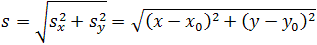Что представляет модуль перемещения при данном движении шарика как направлен вектор перемещения
Лабораторные работы по физике 9 класс
Физика 9. Лабораторная работа №1. Определение обсолютной и относительной погрешностей прямых измерений
Контрольные вопросы:
1) Почему нельзя абсолютно точно измерить прибором физическую величину?
Ответ: Источников погрешностей много: несовершенство приборов, наших органов чувств, влияние внешних факторов (толчки, изменение трения, температуры, электрические и магнитные поля и т. п.), изменение самого измеряемого объекта, неполнота теоретической модели, приближенный характер метода, округление при отсчетах и вычислениях и др. Причины, приводящие к погрешностям измерений, неизбежны. Поэтому неизбежны и сами погрешности. Следовательно, бессмысленно пытаться получить при измерениях абсолютно точный результат. Цель экспериментатора состоит в том, чтобы:
1) определить значение измеряемой величины с возможно меньшей погрешностью;
2) оценить эту погрешность;
3) правильно округлить результат.
Без знания погрешности результат измерения не может иметь ни практической, ни познавательной ценности.
2) Будет ли одинаковой относительная погрешность измерения промежутка времени, если нитку с шариком отклонить на угол 45°? Почему?
Ответ: Совсем непростой вопрос. Учащиеся только в старших классах узнают, что нитка с шариком представляет собой математический маятник, а измеряемый в работе промежуток времени – период маятника. Еще Галилей установил, что период колебаний подобного маятника не зависит от угла начального отклонения от положения равновесия. Позже Гюйгенс записал для периода такого маятника соответствующую формулу. Однако независимость периода от угла отклонения справедлива лишь для малых углов. В 9-м классе этого можно и не знать, а отвечать на вопрос надо. Согласно определению относительная погрешность есть отношение абсолютной погрешности к среднему значению измеряемой величины:
При значительном увеличении угла отклонения нити несколько увеличится путь (дуга окружности), который проходит шарик; изменится и средняя скорость движения шарика. Однако же, несмотря на увеличение средней скорости, нет уверенности, что время останется тем же! Все это приведет к некоторому изменению измеряемого промежутка времени (знаменателя дроби). А значит, изменится и относительная погрешность измерения времени!
3) Если при трех и более повторных измерениях данным прибором получены одинаковые значение физической величины, то чему равны абсолютная случайная и систематическая погрешности? Относительная погрешность?
Ответ: Это никак не повлияет на систематическую погрешность Δtсист= Δtпр+ Δtо, которая связана с несовершенством измерительного прибора и округлением при отсчетах.
Отсутствие же при расчетах случайной погрешности кажущееся, формальное. Случайная погрешность не равна 0 и не отсутствует! Повторение одинаковых значений физической величины свидетельствует о недостаточной чувствительности измерительного прибора. В этих условиях желательно заменить измерительный прибор более чувствительным, способным измерить меньшие промежутки времени.
Что касается относительной погрешности, то формально (но только формально!) она будет меньше, так как не учтена случайная погрешность.
Физика 9. Лабораторная работа №2. Имерение ускорения при равноускоренном движении тела
Контрольные вопросы:
1) Что представляет собой модуль перемещения шарика? Как направлен вектор перемещения шарика? Как направлен вектор перемещения?
Ответ: Так как движение прямолинейное, то модуль перемещения шарика равен измерявшейся в работе длине желоба: от точки А начала движения до точки В цилиндрического упора. Согласно определению вектор перемещения шарика направлен вдоль желоба к цилиндрическому упору.
2) Будут ли равными средние скорости движения шарика на первой и второй половинах пути? Почему?
Ответ: Нет, не будут. Движение шарика равноускоренное. Хорошо видно из графика скорости, что скорость шарика непрерывно увеличивается. Это приводит к тому, что средняя скорость на любом последующем участке пути будет всегда больше, чем средняя скорость на любом предыдущем!
Суперзадание: Во сколько раз отличаются промежутки времени движения шарика на первом и последнем сантиметре пути?
Добавить страницу в закладки:
Физика 9. Лабораторная работа №3. Имерение ускорения при равноускоренном движении тела
Контрольные вопросы:
1) Какие положения шарика (в верхней или нижней частях снимка) целесообразнее брать для определения ускорения? Почему?
Отсюда следует, чем больше измеряемое значение величины х, тем меньше ее относительная погрешность, т.е. тем точнее результат измерения.
Замечание 1. Следует запомнить раз и навсегда: если у вас есть возможность выбора – какое значение величины измерять – следует предпочесть для уменьшения погрешности брать для измерения именно наибольшее значение величины. Более того, стремиться создать такие условия при проведении эксперимента, чтобы значение величины по возможности было достаточно большим в сравнении с неизбежной абсолютной погрешностью.
Замечание 2. Нельзя говорить: «данные в нижней части точнее» или «внизу тело двигалось точнее». Точнее будет измерение пути (!) в нижней части снимка.
2) В каком соотношении будут модули перемещений шарика за равные последовательные промежутки времени?
Ответ: При прямолинейном движении в одном направлении путь равен модулю перемещения тела. А значит, для модулей перемещений будет выполняться найденное в лабораторной работе соотношение для путей: перемещения, проходимые шариком за равные последовательные промежутки времени при прямолинейном равноускоренном движении без начальной скорости, относятся как ряд нечетных чисел.
Замечание 1. Приведем другой простой вариант аналитического доказательства данного утверждения. (Графический способ на основания графика скорости есть в самой лабораторной работе.) Тут важно два момента: нет начальной скорости и ускорение постоянно. Тогда формула пути, проходимого за t секунд имеет вид:
Таким образом, расписываем пути за t и t-1 секунды. Их разность и равна пути, проходимому за t-ую секунду. Получаем:
Выносим a/2 за скобки, раскрываем квадрат (t –1) 2 :
Здесь замечаем, что по сути (2t –1) – это формула нечетных чисел: (2n –1). Eсли вместо t (или n) последовательно подставлять числа по порядку 1, 2, 3, 4 …, то будем получать нечетные числа тоже по порядку. Отсюда выходит, что
Ну, в общем, для последовательных промежутков то ли секунд, то ли минут, неважно,
3) Что представляет собой график зависимости пути от времени движения шарика из состояния покоя? Начертите график.
Ответ: В данном случае шарик движется равноускоренно, его скорость увеличивается. График пути будет таким же, как и график для проекции (модуля) перемещения – одна из ветвей параболы, т.к. направление скорости остается неизменным и модуль перемещения равен пути (см. рис.1).
Замечание 1. Нас просят начертить, но не построить график пути, поэтому, не указывая масштаб, достаточно показать общий вид графика.
Замечание 2. При отсутствии масштаба по осям графики пути от времени движения шарика из состояния покоя или не из состояния покоя (т.е. имеется некоторая начальная скорость) будут выглядеть одинаково при движении шарика в одном направлении, как у нас. Так что условие «из состояния покоя» в данном случае не имеет значения. Дополнительная начальная скорость будет лишь спрямлять параболу.
Замечание 3. График на рис.3, где ось пути направлена вниз, тоже является правильным ответом на поставленный вопрос. Он даже более нагляден, чем график на рис.1. График 3 получен из графика 1 поворотом на 180 0 по часовой стрелке (см. рис.2) и отражением относительно вертикальной оси. Положение начала осей координат в условии можно считать задано точкой 0 – начала отсчета пути, и его нельзя поместить в любую точку изображенной на рис. в лабораторной работе линейки. Иначе график был бы таким, как на рис. 4, что неверно.
Физика 9. Лабораторная работа №6. Проверка закона Гука
Контрольные вопросы:
1) К чему приложены сила упругости пружины и вес груза?
Ответ: Сила упругости возникает в ответ на деформирующую силу, препятствует деформации, возникает в деформируемом теле и в соответствии с 3-им законом Ньютона приложена к телу – источнику деформации (в данном случае к грузу). Вес груза по определению приложен к опоре или подвесу (в нашем случае к пружине) в точке крепления груза. Это под действием силы веса деформируется пружина. Повторим, очевидное: вес груза и сила упругости пружины связаны третьим законом Ньютона, и, соответственно, приложены к разным телам.
Ответ: Нет, не для любого. Деформация должна быть упругой, как того требует закон Гука. А характер деформации (упругая или пластичная) зависит, в том числе от того, насколько велика внешняя сила. Дополнительно сообщим: у образца есть предел пропорциональности, при превышении которого пропорциональность нарушается. Далее – предел упругости. Превышение приводит к пластическим деформациям и, наконец, предел прочности, после которого наступает разрушение образца.
Суперзадание: Как изменится жесткость пружины, если длину пружины уменьшить на одну треть?
Ответ:
Замечание. На самом деле следует говорить «коэффициент жесткости», а не «жесткость», как пишут авторы учебного пособия.
Решение. Здесь можно рассуждать по-разному.
1-й способ. Проще воспользоваться жизненным опытом, который говорит о том, что с уменьшением длины пружины ее жесткость пропорционально возрастает. (Вспомним, например, суперзадание к лаб. работе в 7 кл. по укорачиванию пружины в 2 раза при градуировании пружины динамометра.)
Соответственно можем составить пропорцию:
k2 – коэффициент жесткости после уменьшения длины пружины, длина которой теперь стала 2/3l0.
Можно рассуждать и более строго.
2-й способ. Будем рассматривать пружину как тело начальной длины l0, подвергающееся растяжению. Согласно закону Гука для продольной деформации удлинение ∆l тела пропорционально его начальной длине l0 и приложенной силе F:
где C − коэффициент пропорциональности, зависящий в общем случае от радиуса витков, диаметра проволоки и материала пружины.
Ответ. Увеличится в 1,5 раза.
Физика 9. Лабораторная работа №7. Измерение коэффициента трения скольжения
Контрольные вопросы:
1) Что показывает коэффициент трения скольжения?
Ответ: Для начала надо понять, что физическая величина имеет определение, может нечто характеризовать, что-то показывать, от чего-то зависеть, т.е. требуется четко различать следующие понятия в отношении физической величины: называться, показывать, характеризовать, зависеть (см. далее вопрос №3). Итак, что же показывает коэффициент трения скольжения? Коэффициент трения скольжения определяется как отношение силы трения движущегося тела к силе давления (или к равной ей силе нормальной реакции опоры):
Отсюда, из определения, видно, что коэффициент трения скольжения показывает во сколько раз одна сила больше другой, точнее, какая доля от силы давления, затрачивается на преодоление трения при равномерном движении тела по горизонтальной неподвижной опоре.
Будьте внимательны и постарайтесь понять. Для сравнения с «показывает» приведем ответ на вопрос «Что характеризует коэффициент трения?»
Коэффициент трения характеризует свойства материалов трущейся пары тел (род материала, т.е. из чего состоят соприкасающиеся части тел, жесткости, упругости и др.) и состояние их поверхностей (качество обработки поверхностей, наличие примесей, влажности, грязи и т.п.).
Такова наука. Как отвечать на вопрос «От чего зависит коэффициент трения скольжения?» см. далее ответ на вопрос №3.
Замечание. Ответ на данный вопрос на страницах национального учебного пособия по физике для 9 кл. не найдем! На этот, казалось бы, простой вопрос большинство учащихся и учителей дают неправильный ответ. Поэтому после проверки лабораторной работы Вашим учителем можете сослаться на данный сайт и учителя физики Шинкарева В.М.
2) Почему коэффициент трения скольжения является безразмерной величиной?
Ответ: Ответ на этот вопрос также прямо следует из определения коэффициента трения. Согласно определению, коэффициент трения представляет собой отношение однородных величин: сил. Результат этого отношения будет (считается) в метрологии безразмерной величиной.
3) От чего зависит коэффициент трения скольжения?
Ответ: Коэффициент трения скольжения зависит от:
а) свойств материалов соприкасающихся поверхностей;
б) качества их обработки;
в) относительной скорости движения тел;
г) других факторов, учесть которые возможно пока только экспериментально.
Замечание. Этот вопрос близок по смыслу к вопросу «От чего зависит коэффициент трения скольжения?» Однако, как видим, есть разница. Надо понимать, что трение – результат тонких микроскопических процессов, связанных с атомно-молекулярным строением вещества. То есть трение, как и упругость, обусловлены электромагнитным взаимодействием, однако вывести теоретически значения коэффициента трения и жесткости пока не удается! Поэтому в инженерной практике данные свойства тел рассматриваются как первичные, наряду с инерцией и гравитацией. Таким образом, формула для расчета силы трения со времени ее открытия Амонтоном в 1699 г. таит в себе еще много загадок. Достаточно вспомнить парадоксальную независимость силы трения от площади соприкасающихся поверхностей…
Суперзадание: Как с помощью линейки, бруска с грузами и доски определить коэффициент трения скольжения дерева по дереву?
Ответ: Определить значение коэффициента трения покоя можно следующим образом.
Как известно, μп = Fп max/Fд. (1) Пусть тело (нагруженный плоский брусок) лежит на наклонной плоскости АВ (рис.). На него действуют три силы: сила тяжести F, сила трения покоя Fп и сила реакции опоры N. Нормальная составляющая Fн силы тяжести представляет собой силу давления Fд, производимого телом на опору, т. е. Fн = Fд. (2)
При малых углах наклона a сила Fт уравновешивается силой трения покоя Fп и тело на наклонной плоскости покоится (сила N реакции опоры по третьему закону Ньютона равна по модулю и противоположна по направлению силе Fд, т. е. уравновешивает ее).
Будем увеличивать угол наклона a до тех пор, пока тело не начнет скользить вниз по наклонной плоскости. В этот момент
Подставив в формулу (1) выражения (2) и (3), получим
Подставив эти значения Fт и Fн в формулу (4), получим:
Измерение, исходя из сказанного, сводится к измерению тангенса угла tga = H/L (6), то есть катетов прямоугольного треугольника, для чего и нужна линейка. Таким образом, кладем на доску брусок, нагружаем его, и начинаем поднимать доску за один конец вверх вдоль штатива. Тангенс угла наклона доски к поверхности, при котором брусок только начинает скользить и есть коэффициент трения покоя. Это полезно запомнить! Коэффициент трения скольжения соответствует тангенсу углу, при котором брусок движется равномерно по наклонной доске. Последнее практически и будет происходить при найденном угле, так как коэффициент трения покоя практически равен коэффициенту трения скольжения. Многократно измерив и вычислив отношение средних значений H и L (см. формулу (6)), получим искомое значение коэффициента трения.
Что представляет модуль перемещения
модуль S его перемещения, модуль средней скорости, а также среднепутевую скорость
Катер движется по озеру с постоянной по модулю скоростью 18 км/ч. Сначала в течении 1 минуты 40.
Модуль перемещения
Помогите разобраться с задачей. Качество не ахти, но, пожалуйста, помогите, последняя задача.
найти модуль вектора перемещения
Радиус- вектор материальной точки изменяется по закону : r(t) =t^2*(6i+8j) (cм) Найлидитель модуль.
Определите путь и модуль вектора перемещения
Помогите решить 2 задачи 1. Тело совершает пол оборота(вокруг окружности) определите путь и модуль.
Скажите пожалуйста чему равна
дэльта L отсчета?
Добавлено через 34 минуты
пожалуйста ответьте хоть кто-нибудь прошу пожалуйстааа
А можете еще пожалуйста ответить
1)Какие положения шарика(в верхней или нижней части снимка на рисунки 1) целесообразнее брать для определения модуля ускорения.Почему?
2)В каком соотношение будут модули перемещений шарика за равные последовательные промежутки времени?
Добавлено через 18 секунд
щас я картинку скину
Найти модуль перемещения тела к концу третьей секунды от начала отсчета времени
Уравнение движения тела имеют следующий вид : x=11-4t ; y=3t-1.(все в метрах)Найти модуль.
Модуль cisco VIC-2FXO что из себя представляет и как его настроить
Друзья, помогите понять что из себя представляет модуль cisco VIC-2FXO. Как его настроить? Для чего.
Определить путь и модуль перемещения вертолета
3. Вертолет, пролетев в горизонтальном направлении по прямой 4 км, вернул под углом 90 градусов и.
Кинематика. Перемещение и путь.
Перемещением в механике называют вектор (направленный отрезок прямой), соединяющий начальное и последующее положения тела.
Понятие вектора перемещения вводится для решения задачи кинематики – определить положение тела в пространстве в данный момент времени, если известно его начальное положение.
Допустим, точка М движется по криволинейной траектории и в некоторые моменты времени t1 и t2 оказывается в точках М1 и М2 соответственно. Вектор 


Путь – это длина участка траектории, пройденного телом за данный промежуток времени. В общем случае модуль вектора перемещения не равен длине пути, пройденного телом за некоторый промежуток времени, поскольку траектория может быть криволинейной, а тело может менять направление движения.
Модуль вектора перемещения и путь могут быть равны только при прямолинейном движении в одном направлении. При изменении направления прямолинейного движения модуль вектора перемещения будет меньше пути.
При криволинейном движении модуль вектора перемещения тоже меньше пути, поскольку хорда всегда меньше дуги, которую она стягивает.
Траектория
Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
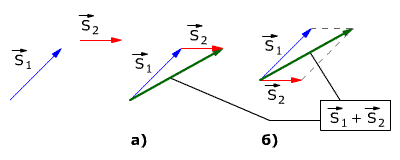
Правило сложения векторов
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Проекции вектора перемещения
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения 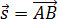
Выберем ось ОХ так, чтобы вектор 
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
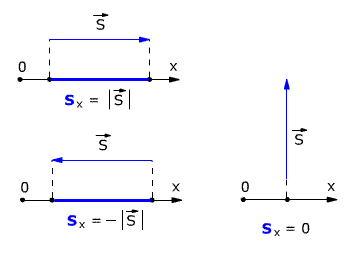
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
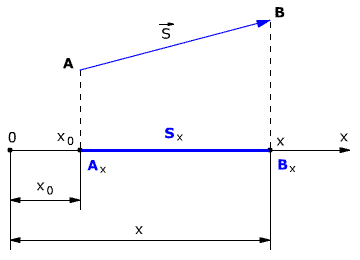
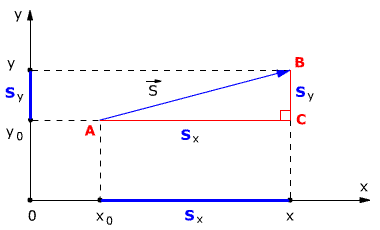
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
По теореме Пифагора
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.