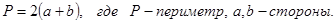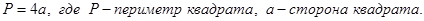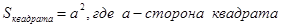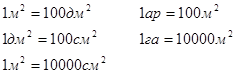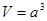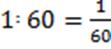Что принимается за единицу объема

Опорные сигналы по теме «Формулы. Площади. Объемы». Математика, 5 класс. Учебник Н.Я.Виленкин

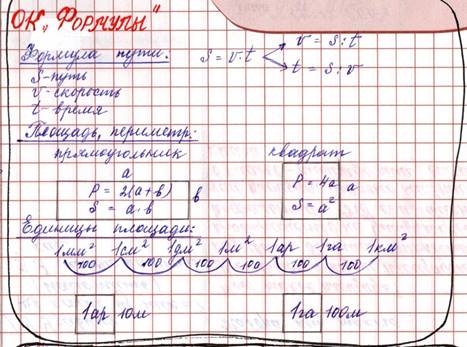
1.Формулой называется запись правила с помощью букв.

2.Формула пути: пройденный путь равен произведению скорости и времени движения.

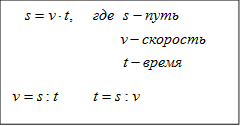
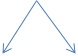3.Периметр прямоугольника равен удвоенному произведению суммы его сторон.

4.Периметр квадрата равен произведению его стороны на число 4.

5.За единицу площади принимается квадрат, у которого сторона равна 1

· Площади равных фигур равны.

· Площадь всей фигуры равна сумме площадей её частей.

7.Площадь квадрата равна квадрату его стороны.

8.Площадь прямоугольника равна произведению его сторон.

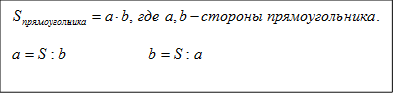
9.Единицы измерения площадей: 1 кв.см, 1 кв.дм, 1кв.мм, 1 кв.м, 1 га, 1 кв.км.

10.1ар – площадь квадрата со стороной 10 м.

11.1 га – площадь квадрата со стороной 100 м.

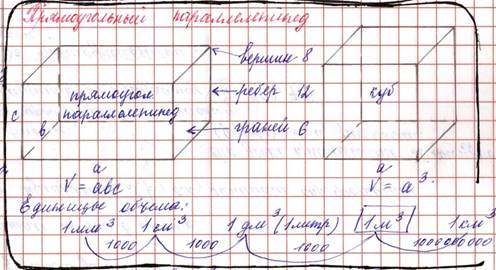
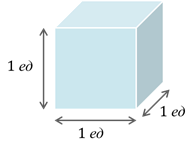
12.За единицу объемов принимается куб, у которого сторона равна 1.

13.Единицы измерения объемов: 1 куб. мм, 1 куб. см, 1 куб. дм. или 1 литр, 1 куб. м, 1 куб. км.

14.Объем прямоугольного параллелепипеда равен произведению длины, ширины и высоты. V=a∙b∙c

15. Объем куба равен кубу его ребра.

Лист взаимоконтроля по теме «Формулы. Площади. Объемы» (§4)

Источник

Понятие объема

Урок 21. Геометрия 11 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Понятие объема»

На этом уроке мы поговорим об объеме тел. Выясним основные свойства объёма.

В повседневной жизни очень часто нам приходится сталкиваться с понятием объёма. Например, нас интересует объём (вместимость) коробки или банки.

А в практической деятельности человеку необходимо уметь вычислять объём при изготовлении каких-либо деталей.

Или при строительстве различных сооружений.

Ведь многие строительные объекты и детали конструкций имеют форму геометрических тел: параллелепипедов, призм, пирамид, шаров и т.д.

Итак, мы с вами продолжаем изучать стереометрию. Напомним, что стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Как вы уже поняли, пространственные фигуры, или как их ещё называют тела, в отличие от плоских фигур, обладают вместимостью, т.е. они имеют объём. Такие фигуры называют объёмными.

А значит, мы можем найти объём тела. Давайте разберёмся, как же мы будем его вычислять.

Из курса планиметрии вы уже знакомы с понятием площади многоугольника. Каждый многоугольник имеет площадь, которая измеряется с помощью выбранной единицы измерения площадей.

В качестве единицы измерения площадей обычно берут квадрат, сторона которого равна единице измерения отрезков.

Напомним, что площадь – это положительная величина, определенная для каждого многоугольника, числовое значение которой обладает следующими свойствами:

1) площадь квадрата, сторона которого равна единице измерения длины, равна единице.

2) равные многоугольники имеют равные площади.

3) если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Процедура измерения объёмов аналогична процедуре измерения площадей. Будем понимать объём как количество занимаемого геометрическим телом пространства. При выбранной единице измерения объём тела выражается положительным числом, которое показывает, сколько единиц измерения объёмов и её частей укладываются в этом теле.

Чтобы измерить объем, надо выбрать единицу измерения объёмов. Единицей объёма является объём куба с ребром, равным единице.

Такой куб называется единичным. Объём единичного куба принимается за единицу измерения объёмов.

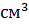
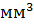
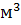
Например: объём куба с ребром, равным 1сантиметру, равен одному кубическому сантиметру, пишут так: 1 куб. см, или так 1 . Точно также определяются и кубический миллиметр (1 ), кубический метр (1 ) и так далее.

Нетрудно заметить, что название единицы объёма получается из названия единицы длины присоединением прилагательного «кубический».

Находя объём тела, мы фактически выясняем, сколько единичных кубов он содержит.

Проще всего измерить объём прямоугольного параллелепипеда.

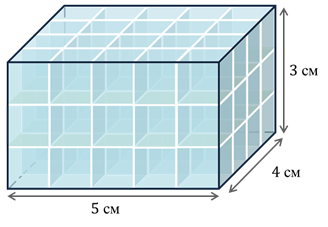
Пусть дан прямоугольный параллелепипед с измерениями: длина – 5 см, ширина – 4 см и высота – 3 см.

Посчитаем, сколько единичных кубов с ребром 1 см вмещается в нём. Для этого разобьём параллелепипед плоскостями, параллельными основаниям, на 3 слоя высотой в 1 см.

Понятно, что для того чтобы заполнить весь прямоугольный параллелепипед, нужно вложить в него 3 одинаковых слоя с единичными кубами, т.к. высота параллелепипеда 3 см. Посмотрим сколько единичных кубов заполнят первый слой.

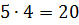
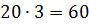
Видим, всего в первом слое поместилось ед. кубов. Но у нас же 3 одинаковых слоя. А, значит, в трёх таких слоях будет помещаться ед. кубов.

Следовательно, объём указанного параллелепипеда равен 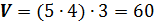(см 3 ).

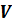
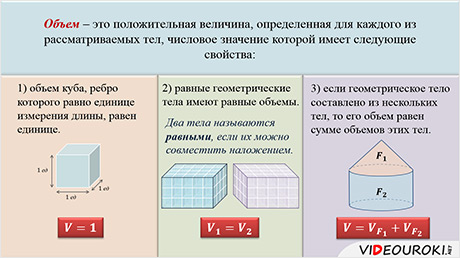
Напомним, что объём обозначается заглавной латинской буквой , которая является сокращением от латинского слова volume – что в переводе обозначает «объём», «наполнение».

Итак, объём – это положительная величина, определённая для каждого из рассматриваемых тел, числовое значение которой имеет следующие свойства:

1) объём куба, ребро которого равно единице измерения длины, равен единице.

2) равные геометрические тела имеют равные объёмы.

Равенство двух фигур, в частности двух тел, в стереометрии определяется так же, как и в планиметрии: два тела называются равными, если их можно совместить наложением.

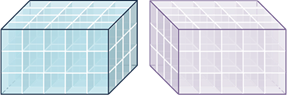
На экране изображены два прямоугольных параллелепипеда с соответственно равными измерениями. Так как их измерения соответственно равны, то каждый из них содержит столько же единиц измерения объемов, сколько и второй.

3) если геометрическое тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

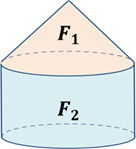
На экране изображено тело, составленное из нескольких тел, причем внутренние области этих тел не имеют общих точек, но имеют общие граничные точки. Наше тело состоит из цилиндра и конуса. Общими граничными точками этих тел будут точки их общего основания. Понятно, что объём всего тела складывается из объемов составляющих его тел.

Второе и третье свойства называются основными свойствами объёмов.

Справедливо следующее следствие из этих свойств.

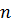
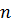
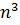
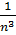
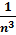
Рассмотрим куб, принятый за единицу измерения объёмов. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на равных частей ( – произвольное целое число) и проведём через точки разбиения плоскости, перпендикулярные к этому ребру. Куб разобьётся на равных маленьких кубов с ребром . Так как сумма объёмов всех маленьких кубов равна объёму всего куба, т.е. равна единице, то объём каждого из маленьких кубов равен . Тогда имеем, объём куба с ребром равен .

Давайте ответим на несколько несложных вопросов.

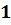
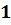
Первый вопрос: на сколько кубиков с длиной ребра дм можно распилить куб с ребром м?

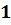
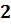
Второй вопрос: сколько кубиков с длиной ребра см содержит прямоугольный параллелепипед с размерами см на см на см?

И третий вопрос: сколько кубиков содержится в кубике Рубика?

Ответ: обратите внимание, на экране изображён кубик Рубика.

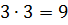
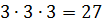
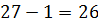
Каждый слой кубика Рубика содержит маленьких кубиков. Всего он имеет 3 таких слоя. Значит, весь кубик Рубика должен состоять из маленьких кубиков. Но на самом деле их: , т.к. вместо центрального кубика – механизм крепления, за счет которого вращаются кубики.

На этом уроке мы говорили об объёме, одной из важных величин, связанной с геометрическими телами.

Объём – это положительная величина, определенная для каждого из рассматриваемых тел, числовое значение которой имеет следующие свойства:

1) равные геометрические тела имеют равные объёмы.

2) если геометрическое тело составлено из нескольких тел, то его объем равен сумме объёмов этих тел.

3) объём куба, ребро которого равно единице измерения длины, равен единице.

Источник

1.1.3. Меры массы и объема, используемые в аптечной практике и применении лекарств

Лекарственные вещества животным назначаются в определенных количествах, называемых дозой, выраженных в массовых, объемных единицах или в единицах биологической активности. За единицу массы принимается грамм. Обозначение выполняется арабскими цифрами, система измерения – десятичная. Для взвешивания лекарственных веществ в аптечной практике прменяются: весы ручные (предельный вес 1–5 г, минимальный 0,01-0,02 г; предельный вес 10-100 г, минимальный 0,05 г), тарирные (предельный вес 0,5–1 кг, минимальный 1 г), тарелочные (предельный вес 2–5 кг, минимальный 1 г), электронные, аналитические.

При взвешивании необходимо соблюдать следующие правила:

1) пользоваться только проверенными и клейменными весами и разновесами;

2) перед взвешиванием проверять точность показания весов, чистоту их и разновесов;

3) разновесы класть на левую чашку весов, а взвешиваемое вещество – на правую; миллиграммовый разновес брать только пинцетом;

4) порошки отвешивать на бумажных капсулах, а жидкости – в предварительно взвешенных склянках;

5) не загрязнять чашки весов лекарственными веществами, не ставить на них горячие, загрязненные склянки и предметы;

6) после взвешивания повторно проверить вес лекарственного вещества по разновесу.

При приготовлении жидких лекарственных форм используется бюреточная система, включающая комплект измерительных приборов (бюретки, пипетки, мерные цилиндры, колбы). Мерные приборы для бюреточной системы выпускаются в виде нескольких наборов (от 8 до 20 бюреток и такого же количества пипеток), градуированных в объемном измерении (в миллилитрах) применительно к каждой используемой жидкости согласно ее удельному весу. Поэтому на каждой бюретке указывается название жидкости, для отмеривания которой она предназначена. В объемных измерениях берутся и растворители. За единицу объема в рецептуре принят миллилитр.

Растворы и другие жидкие лекарственные формы для внутреннего применения отмеривают градуированными мензурками в миллилитрах, цилиндрами или условными мерами (ложками, стаканами). При этом исходят из того, что жидких лекарственных веществ (воды) содержится: в чайной ложке 4–5 мл, в десертной 8-10, в столовой 15–20, в стакане 200–250 мл. Концентрированные растворы солей и экстракты тяжелее воды на 20^0 %, а масло легче на 20–25 %.

Данный текст является ознакомительным фрагментом.

Источник

Методика работы с заданием, направленным на отработку приёма решения задач на совместную работу, когда объём работы принимается за единицу

Методика работы с заданием, направленным на отработку приёма

решения задач на совместную работу, когда объём работы принимается за единицу

Просмотр содержимого документа
«Методика работы с заданием, направленным на отработку приёма решения задач на совместную работу, когда объём работы принимается за единицу»

Методика работы с заданием, направленным на отработку приёма

решения задач на совместную работу, когда объём работы принимается за единицу

Учебник: Г. В. Дорофеев и др.

Цель: освоить приём решения задач на совместную работу, когда объём работы принимают за единицу.

Ход фрагмента урока:

Анализ условия задачи

— Ребята, откройте учебники на странице 134, прочитайте задачу № 612. С чего начинается работа над любой задачей?

— С анализа условия и составления краткой записи

— Какие вопросы мы задаём на этом этапе?

— Какого типа задача? О каких объектах идёт речь? Какими величинами характеризуется задача и какова связь между ними?

— Кто хотел бы пойти к доске и провести анализ условия задачи, составить краткую запись?

— Один из учащихся выходит к доске, вслух проводит анализ условия и составляет краткую запись

— Какого типа эта задача? (Задача на совместную работу)

— О каких объектах идёт речь? (В задаче идёт речь о работе мастера и его ученика)

— Какими величинами характеризуется работа? (Временем, производительностью, объёмом работы; )

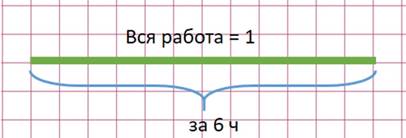
— Что известно о работе мастера? (Он 1) выполняет всю работу 2) за 3 часа)

— Что известно о работе ученика? (Он 1) выполняет всю работу 2) за 6 часов)

— Что требуется найти? ( 1) часть работы, которую выполняет каждый из них за 1 час; 2) часть работы, которую они выполнят совместно за 1 час; 3) время, за которое они выполнят всю работу, работая совместно).

Параллельно с беседой составляется краткая запись.

Источник

Делаем записи в тетради, выделено жирным текстом.

Запись в тетради Тема урока «Решение задач на совместную работу»

Теоретический материал для самостоятельного изучения

На предыдущих уроках мы научились выполнять арифметические действия с обыкновенными дробями. Сегодня мы рассмотрим, как с помощью обыкновенных дробей решать задачи на совместное выполнение некоторой работы.

Под совместной работой можно понимать абсолютно любое действие: и одновременный поток воды из двух труб при наполнении бассейна, и изготовление деталей двумя рабочими, и вспашку поля несколькими тракторами, и набор текста на компьютере.

Всю работу мы будем принимать за единицу. 1

А объём выполненной работы выражать как часть этой единицы.

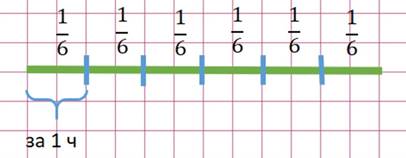
Если какая-то работа выполняется за шесть часов, то за час выполняется одна шестая часть этой работы

.

Общая производительность – объём работы, выполняемый совместно всеми работниками за единицу времени.

Мы с вами знаем, что именно в этом дворе хотят построить плотники? (нет)

— Тогда весь двор (всю работу) мы примем с вами за единицу.

1) Какую часть работы сделает первый плотник за год?

1 ׃ 3 = 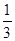(двора)

2) Какую часть работы сделает второй плотник за год?

1 ׃ 6 = 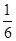(двора)

3) Какую часть работы сделают оба плотника вместе за год?

(двора)

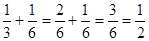
4) За сколько времени сделают они всю работу, если будут работать совместно?

1 ׃ 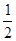= 2 (года)

Ответ: Два плотника поставят двор, работая вместе за 2 года.

Алгоритм решения задач на совместную работу.

Запись в тетради Алгоритм решения задач на совместную работу

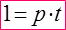Всю работу («Целое») принимаем за 1,

3. общая производительность Р = Р₁ + Р₂

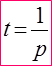Время работы

при совместной работе складываются не время работы, а часть работы, которую делают ее участники за единицу времени (год, месяц, день, час и т.д.), а вся выполняемая работа принимается за 1 – «целое».

Одна труба заполняет бассейн за 60 минут, а вторая – за 20 минут. За сколько минут заполнится бассейн при включении обеих труб?

Запись в тетради:

Дата добавления: 2020-11-15 ; просмотров: 103 ; Мы поможем в написании вашей работы!

Источник