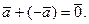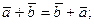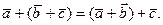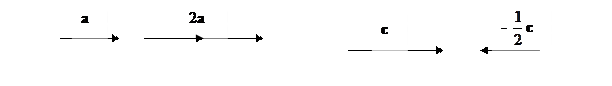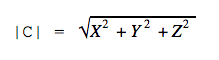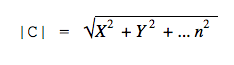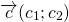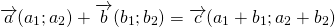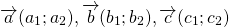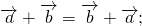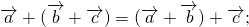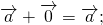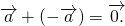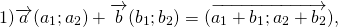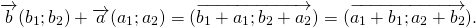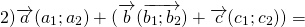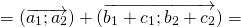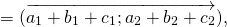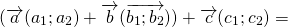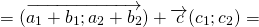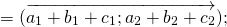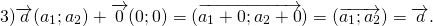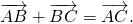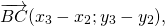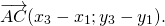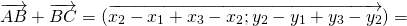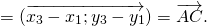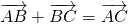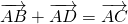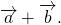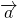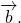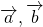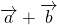Что принимается за сумму векторов вектор или число

Сумма векторов

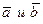
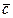
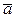
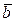
Определение. Суммой векторов называется такой вектор , начало которого совпадает с началом вектора , а конец – с концом вектора (правило треугольника).

Из определения следует, что сумма двух противоположных векторов равна нулевому вектору:

Сложение векторов подчиняется следующим законам:

а) переместительному закону

б) сочетательному закону

Операция сложения может быть распространена на любое число слагаемых векторов.

Для того чтобы сложить n векторов, надо к концу первого вектора приложить начало второго, затем к концу второго вектора приложить начало третьего и т.д. и, наконец, приложить к концу предпоследнего вектора начало последнего; тогда замыкающий вектор, соединяющий начало первого вектора с концом последнего, и будет являться вектором-суммой данных векторов.

При сложении векторов можно любым образом переставлять и группировать слагаемые.

Источник

СУММА ВЕКТОРОВ И ПРОИЗВЕДЕНИЕ ВЕКТОРА НА ЧИСЛО

ТЕМА 1. ВЕКТОРНАЯ АЛГЕБРА

Программы письменных теоретических опросов(на 10 минут)

Первый теоретический опрос.

Знать определения: направленного отрезка, нулевого направленного отрезка, длины направленного отрезка, коллинеарных направленных отрезков, сонаправленных и противоположно направленных направленных отрезков, вектора, длины вектора, коллинеарных векторов, сонаправленных и противоположно направленных векторов, противоположных векторов, вектора параллельного плоскости, компланарных векторов. Суммы векторов, разности векторов, произведения вектора на число.

Знать формулировки: свойства сложения векторов, свойства произведения вектора на число, теорему о разности векторов, теорему о коллинеарных векторах, теорему о компланарных векторах.

Второй теоретический опрос.

Знать определения: системы линейно зависимых и линейно независимых векторов, базиса векторного пространства, ортонормированного базиса, координат вектора в данном базисе, угла между векторами, скалярного произведения векторов.

Знать формулировки: свойства систем линейно зависимых и линейно независимых систем векторов, теоремы 1, 2, 3 о линейной зависимости систем из одного двух и трех векторов и следствия из них, теорема о координатах вектора, теорему о вычислении скалярного произведения в ортонормированном базисе и следствия из нее, свойства скалярного произведения векторов.

СУММА ВЕКТОРОВ И ПРОИЗВЕДЕНИЕ ВЕКТОРА НА ЧИСЛО

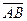
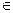
Вектором называется множество всех направленных отрезков пространства, любые два из которых сонаправлены и имеют равные длины, эти направленные отрезки будем называть представителями вектора а. Векторы будем обозначать жирными буквами, например, вектор а, Если направленный отрезок а, то вектор а можно обозначать АВ.

Длиной вектора называется длина любого его представителя.

Векторы а и b называются сонаправленными, если любые два их представителя сонаправленны, будем обозначать сонаправленные векторы так: а ↑↑b. Векторы а и b называются противоположно направленными, если любые два их представителя противоположно направлены, будем обозначать противоположно направленные векторы так: а ↑↓b.

Вектор называется параллельным прямой, если любой его представитель либо параллелен прямой, либо лежит на этой прямой. Два вектора а и b называются коллинеарными, если они параллельны одной прямой. Коллинеарные векторы будем обозначать так а││ b.

Вектор называется параллельным плоскости, если любой его представитель либо параллелен плоскости, либо лежит в этой плоскости. Три и более векторы называются компланарными, если они параллельны одной плоскости. (Любые два вектора компланарны)

Если дан вектор а и точка О, то существует единственная точка А, такая, что АВ = а, будем в этом случае говорить, что вектор а отложен от точке А. Договоримся под словами «построить вектор а» понимать отложить вектор а от какой либо точки О, т.е. построить точку А такую, что а = ОА.

Противоположными векторами называются такие два вектора, которые противоположно направлены и длины которых равны. Вектор, противоположный вектору а, обозначается так (— а).

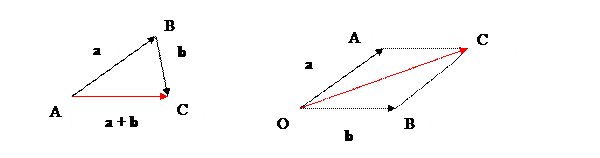
Суммой векторов а иb называется вектор с, который получается следующим образом: от произвольной точки А отложим вектор АВ = а, от точка В отложим вектор ВС =b, тогда с = а +b = АС. Указанное в этом определении правило сложения векторов называется правилом треугольника. (Рис. 1) Если векторы а и b не коллинеарны, то можно от произвольной точки О отложит векторы ОА = а иОВ =b, построить параллелограмм ОАСВ, тогда вектор ОС = а +b. Сложение векторов по этому правилу называется правилом параллелограмма (Рис. 2)

Сложение векторов обладает следующими свойствами:

1°. Для любого вектора а а + 0 = 0 + а.

2°. Для любого вектора а а + (- а) = (- а) + а = 0.

3°. Для любых векторов а и ba + b = b + a (свойство коммутативности).

4°. Для любых трех векторов a, b, c (a + b)+ c = a + (b + c) (свойство ассоциативности).

Произведением числоλ на вектор а(или произведением вектора а на число λ )будем называть вектор b = λ а, удовлетворяющей двум условиям: 1)длина вектора b равна произведению модуля числа λ и длины вектора а │b│= │ λ ││а│, 2) если λ 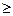0, то вектор b сонаправлен с вектором а, если λ

Произведение вектора на число обладает следующими свойствами:

1°. Для любого вектора а 1 а = а.

2°. Для любого вектора а 0 а = а.

3°. Для любого вектора а и любых чисел λ и β (λ β) а = λ (β а).

4°. Для любого вектора а и любых чисел λ и β (λ+ β) а = λ а + β а.

5°. Для любых векторов а и b любого числа λ λ(a + b) = λa + λb.

Для решения задач данного раздела целесообразно придерживаться следующих рекомендаций: а) если надо построить алгебраическую сумму векторов, то все векторы со знаками минус заменяем на противоположные векторы со знаками плюс, б) сумма п векторов не изменится, если поменять местами любые два вектора, в) для построения суммы п векторов строим эту сумму по правилу п-угольника, т.е. сначала выбираем направленный отрезок из первого вектора, затем от его конца откладываем направленный отрезок из второго вектора, затем от конца этого отрезка откладываем направленный отрезок из третьего вектора и так далее, тогда соединив начало первого направленного отрезка с концом последнего направленного отрезка, получим направленный отрезок из искомой суммы.

ЗАДАЧА № 1

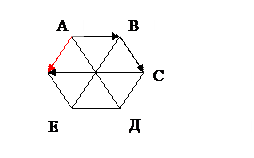
Дан правильный шестиугольник АВСДEF с центром О. Построить вектор

АВ – EF +2ОF.

1) АВ – EF +2ОF = АВ + FE+2ОF

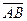
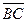
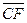
2) Рассмотрим направленный отрезок , от точки В отложим направленный отрезок из вектора FE,затем от точки С отложим направленный отрезок из вектора 2ОF.

Тогда АВ – EF +2ОF = АF.

ОТВЕТ. Искомая сумма равна вектору АF.

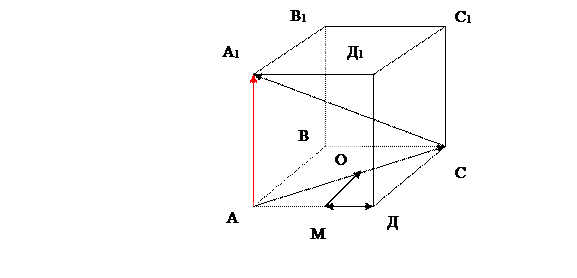
ЗАДАЧА № 2.

— ½ С₁А₁ +СА₁ – ДА + ½ (СВ – В₁А₁)

1) – ½ С₁А₁ +СА₁ – ДА + ½ (СВ – В₁А₁) = ½ А₁С₁ +СА₁ + АД+ ½ СВ + ½ А₁В₁

2) Поменяем местами слагаемые ½А₁С₁ +СА₁ + АД+ ½ СВ + ½ А₁В₁ =

АД +½СВ +½А₁В₁ + ½А₁С₁ + СА₁

3) Откладываем направленные отрезки из данных векторов следующим образом:

АД, ½СВ, ½А₁В₁, ½А₁С₁, СА₁, где М – середина АД, О = АС ВД.

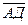
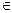
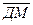
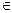
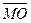
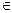
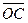
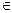
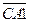
АД +½СВ +½А₁В₁ + ½А₁С₁ + СА₁ = АА₁.

Замечание. Задачи такого типа имеет разные пути решения, но ответ должен быть один и тот же.
При решении данной задачи можно было рассуждать следующим образом:

– ½ С₁А₁ +СА₁ – ДА + ½ (СВ – В₁А₁) = ½ А₁ С₁ +СА₁ + АД + ½ (СВ +

А₁ В₁) = ½ АС + СА₁ + АД + ½ (СВ + ДС) = ½ АС + СА₁ + АД + ½ ДВ =

ОС + СА₁ + АД + ДО = (ДО + ОС) + СА₁ + АД = ДС + СА₁ + АД=

Существуют и другие пути построения искомого вектора.

ОТВЕТ. Искомая сумма равна вектору АА₁.

Источник

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Сложение

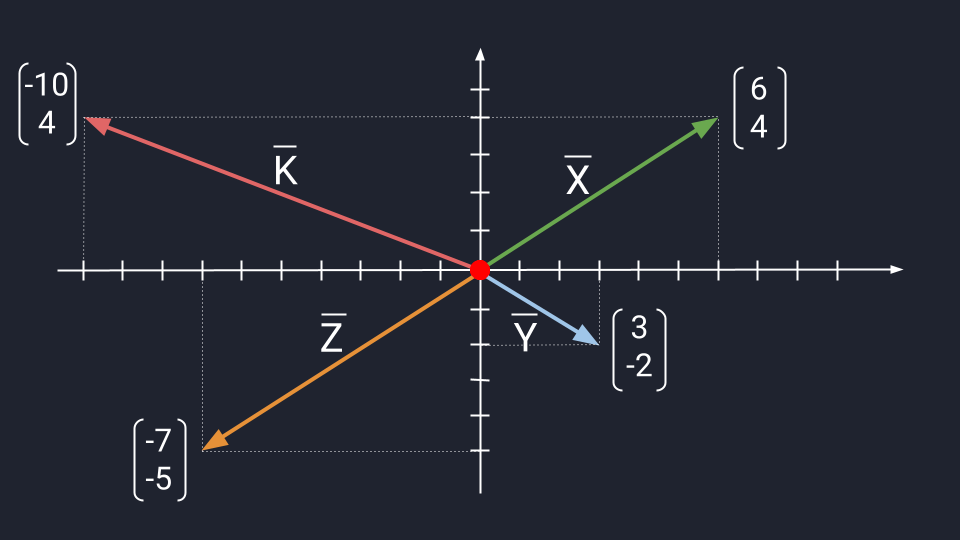
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

Векторы X, Y, Z, K в двухмерном пространстве

Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

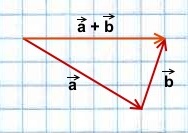
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

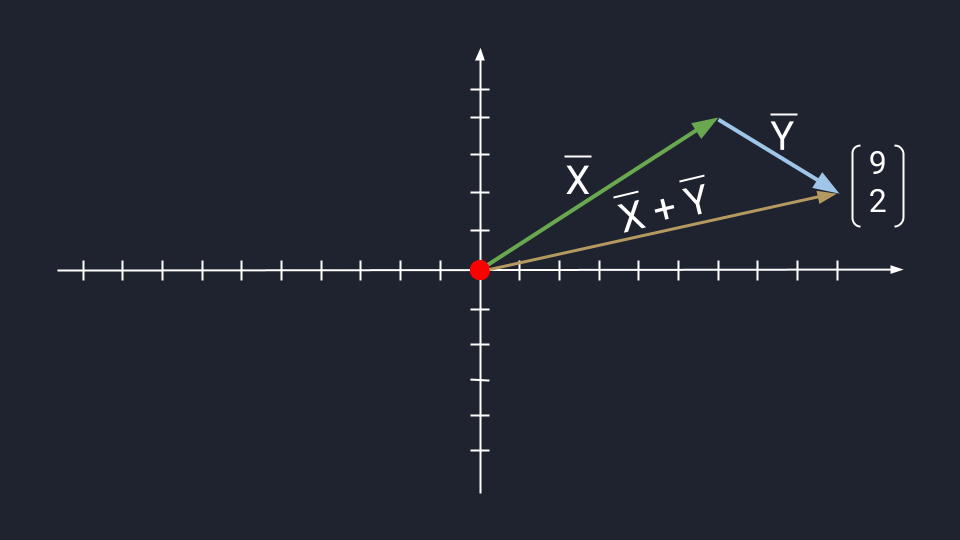
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

Вычитание

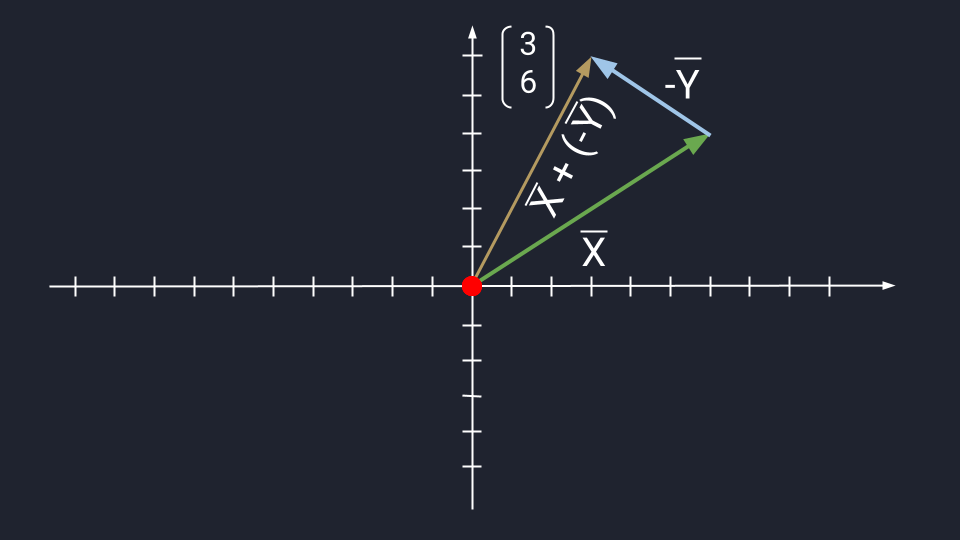
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

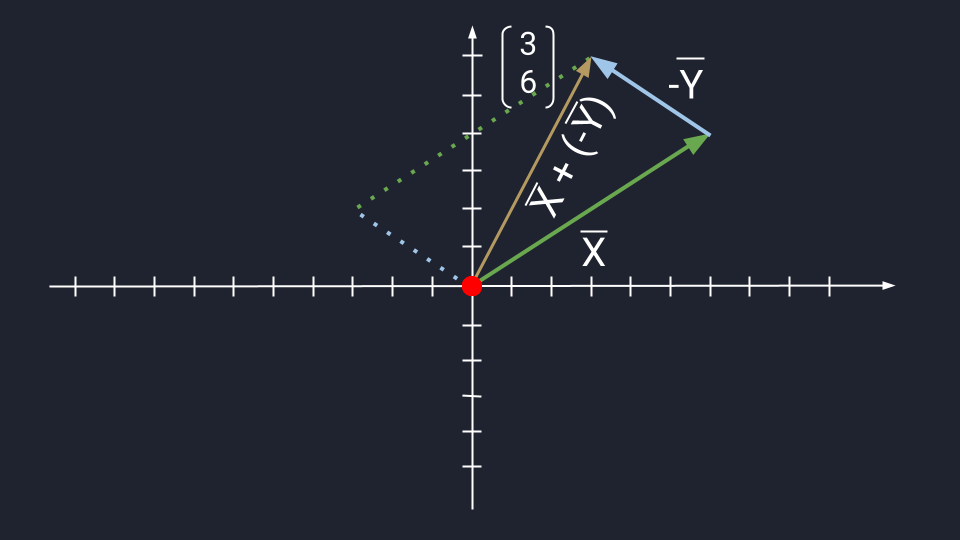
Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 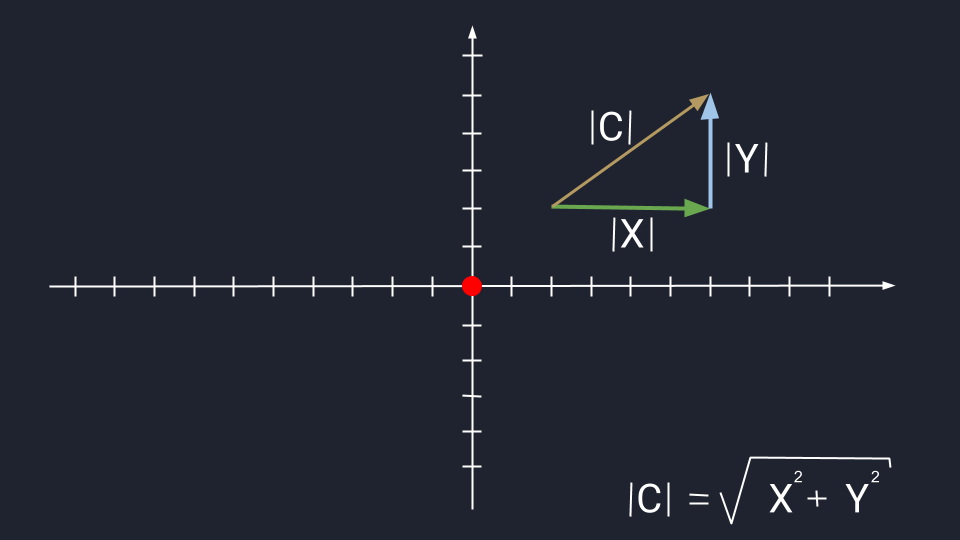Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

Умножение и деление вектора на число

Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

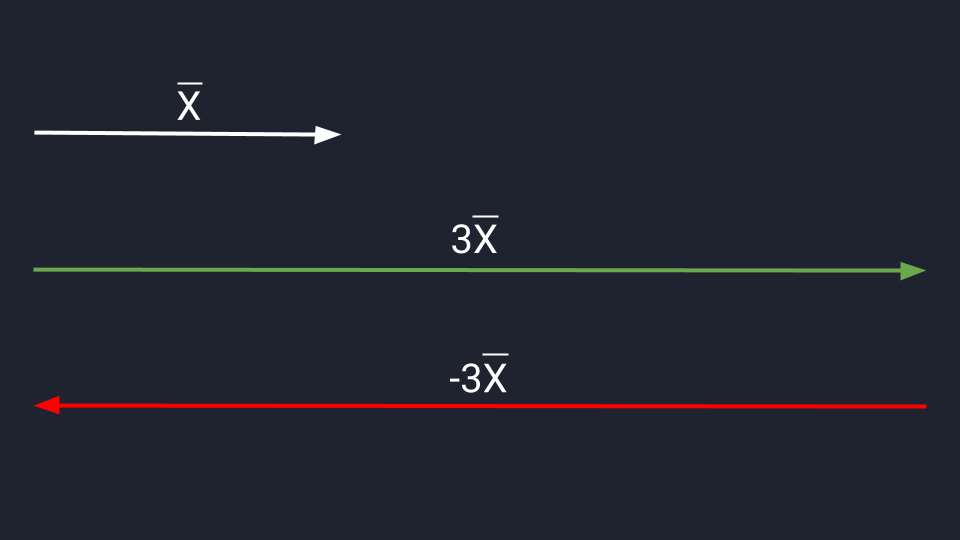
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

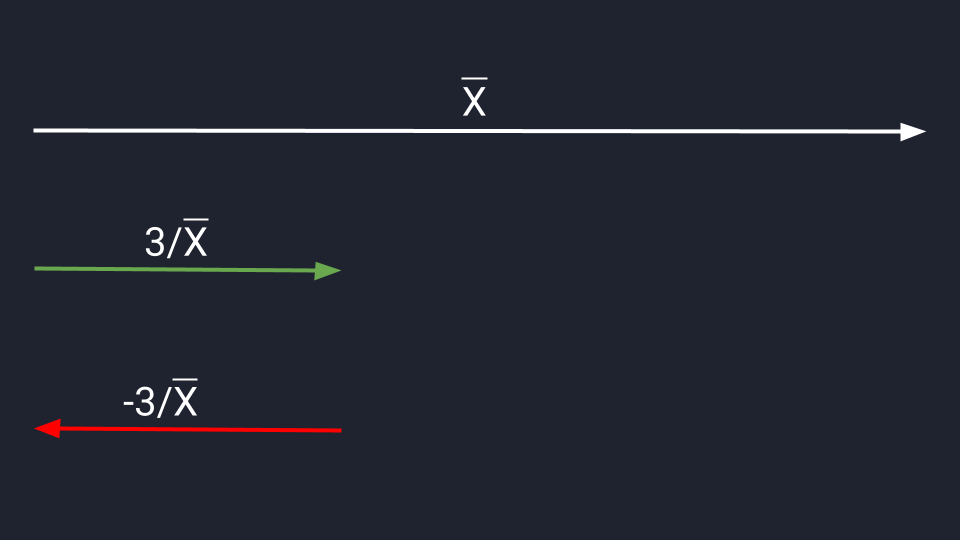
Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

Источник

Сложение векторов

Сумма векторов

Свойства сложения векторов:

Для любых векторов

3) свойство прибавления нулевого вектора:

4) сумма противоположных векторов равна нулевому вектору:

Достаточно сравнить координаты векторов, стоящих в левой и правой частях этих равенств:

Так как соответствующие координаты равны, то эти векторы равны.

(О сложении векторов)

Каковы бы ни были точки A, B, C, имеет место векторное равенство:

Что и требовалось доказать.

Правило треугольника построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу треугольника, надо от конца одного вектора отложить другой вектор и провести вектор от начала первого к концу второго вектора.

Например,

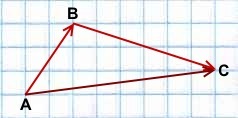
(то есть это правило следует из теоремы о сложении векторов).

Правило параллелограмма построения суммы двух векторов

Чтобы построить сумму двух векторов по правилу параллелограмма, надо отложить эти векторы от общего начала. Сумма векторов есть диагональ параллелограмма, построенного на этих векторах и имеющая с ними общее начало.

Например,

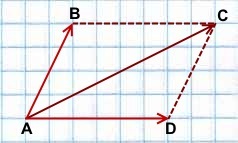
Правило параллелограмма построения суммы векторов применяется лишь для неколлинеарных векторов.

При любом способе построения суммы неколлинеарных векторов получим одинаковый результат.

Построить сумму векторов

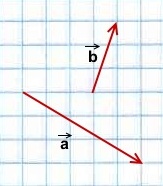
1) Чтобы построить сумму векторов по правилу треугольника, отложим от конца вектора

Сумма этих векторов равна вектору, проведённому от начала первого вектора (a) к концу второго (b).

2) Чтобы построить сумму векторов по правилу параллелограмма, отложим векторы

Достроим на этих векторах параллелограмм.

Сумма

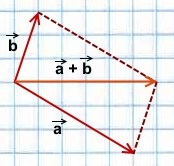
равна вектору, лежащему на диагонали параллелограмма и имеющему с ними общее начало.

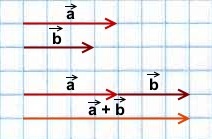
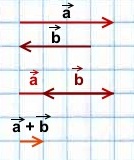
1) Сумма двух сонаправленных коллинеарных векторов равна вектору, сонаправленному этим векторам, длина которого равна сумме длин данных векторов.

2) Сумма двух противоположно направленных векторов равна вектору, направление которого совпадает с направлением вектора, модуль которого больше, а длина равна разности этих векторов.

Фактически в обоих случаях мы используем правило треугольника сложения векторов:

от конца первого вектора откладываем вектор, равный второму, и строим сумму как вектор в направлении от начала первого вектора к концу второго.

Из неравенства треугольника следует ещё два свойства сложения векторов:

Источник