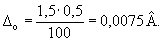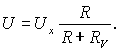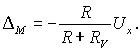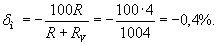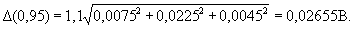Что принимают за абсолютную погрешность в случае однократных прямых измерений
Оценивание погрешностей прямых однократных измерений.
Классификация измерений.
По количеству измерений измерения делятся на однократные и многократные.
По методам получения результатов измерения делятся на прямые, косвенные, совокупные и совместные.
Методы измерений.
Все методы измерений подразделяются на две группы: методы непосредственной оценки и методы сравнения. Методы сравнения в свою очередь включают в себя метод противопоставления, дифференциальный метод, нулевой метод, метод замещения и метод совпадений.
При методе непосредственной оценки значение измеряемой величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия (измерительный прибор, в котором предусмотрено одно или несколько преобразований сигнала измерительной информации в одном направлении, т. е. без обратной связи). На этом методе основаны все показывающие (стрелочные) приборы (вольтметры, амперметры, ваттметры, счетчики электрической энергии, термометры, тахометры и т. п.). При использовании данного метода измерений мера как вещественное воспроизведение единицы измерения, как правило, непосредственно в процессе измерения не участвует. Сравнение измеряемой величины с единицей измерения осуществляется косвенно путем предварительной градуировки измерительного прибора с помощью образцовых мер или образцовых измерительных приборов.
Точность измерения по методу непосредственной оценки в большинстве случаев невелика и ограничивается точностью применяемых измерительных приборов.
Нулевой метод позволяет получить высокие точности измерений и широко используется, например, при измерениях электрического сопротивления мостом с полным его уравновешиванием или постоянного напряжения компенсатора постоянного тока.
Методом замещения называется метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Это, например, взвешивание с поочередным помещением массы и гирь на одну и ту же чашку весов. Метод замещения можно рассматривать как разновидность дифференциального или нулевого метода, отличающуюся тем, что сравнение измеряемой величины с мерой производится разновременно.
Погрешности измерений.
Абсолютная погрешность— это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.
Абсолютная погрешность вычисляется по следующей формуле:
Абсолютная погрешность меры— это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.
Относительная погрешность— это число, отражающее степень точности измерения.
Относительная погрешность вычисляется по следующей формуле:
Относительная погрешность выражается в процентах.
Приведенная погрешность— это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.
Нормирующее значение определяется следующим образом:
1) для средств измерений, для которых утверждено номинальное значение, это номинальное значение принимается за нормирующее значение;
2) для средств измерений, у которых нулевое значение располагается на краю шкалы измерения или вне шкалы, нормирующее значение принимается равным конечному значению из диапазона измерений. Исключением являются средства измерений с существенно неравномерной шкалой измерения;
3) для средств измерений, у которых нулевая отметка располагается внутри диапазона измерений, нормирующее значение принимается равным сумме конечных численных значений диапазона измерений;
4) для средств измерения (измерительных приборов), у которых шкала неравномерна, нормирующее значение принимается равным целой длине шкалы измерения или длине той ее части, которая соответствует диапазону измерения. Абсолютная погрешность тогда выражается в единицах длины.
Погрешность измерения включает в себя инструментальную погрешность, методическую погрешность и погрешность отсчитывания. Причем погрешность отсчитывания возникает по причине неточности определения долей деления шкалы измерения.
Методическая погрешность— это погрешность, возникающая по следующим причинам:
1) неточность построения модели физического процесса, на котором базируется средство измерения;
2) неверное применение средств измерений.
Субъективная погрешность— это погрешность возникающая из-за низкой степени квалификации оператора средства измерений, а также из-за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.
Основная погрешность— это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).
Дополнительная погрешность— это погрешность, которая возникает в условиях несоответствия значений влияющих величин их нормальным значениям, или если влияющая величина переходит границы области нормальных значений.
Аддитивная погрешность— это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).
Мультипликативная погрешность— это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям.
Надо заметить, что значение абсолютной аддитивной погрешности не связано со значением измеряемой величины и чувствительностью средства измерений. Абсолютные аддитивные погрешности неизменны на всем диапазоне измерений.
Значение абсолютной аддитивной погрешности определяет минимальное значение величины, которое может быть измерено средством измерений.
Значения мультипликативных погрешностей изменяются пропорционально изменениям значений измеряемой величины. Значения мультипликативных погрешностей также пропорциональны чувствительности средства измерений Мультипликативная погрешность возникает из-за воздействия влияющих величин на параметрические характеристики элементов прибора.
Систематическая погрешность— это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины. Обычно систематическую погрешность пытаются исключить возможными способами (например, применением методов измерения, снижающих вероятность ее возникновения), если же систематическую погрешность невозможно исключить, то ее просчитывают до начала измерений и в результат измерения вносятся соответствующие поправки. В процессе нормирования систематической погрешности определяются границы ее допустимых значений. Систематическая погрешность определяет правильность измерений средств измерения (метрологическое свойство).
Оценивание погрешностей прямых однократных измерений.
Прямые однократные измерения с приближенным оцениванием погрешностей
При приближенной оценке погрешностей, как и при точной, необходимо перед началом измерений провести предварительную оценку составляющих погрешности результата измерения. Эту информацию получают из опыта проведения подобных измерений, нормативно технической документации на используемые средства измерений и других источников. Если оценка погрешности превышает допустимую, то следует выбрать более точное средство измерений или изменить методику измерения.
Р 50.2.038-2004 ГСИ. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ
Государственная система обеспечения
единства измерений
ИЗМЕРЕНИЯ ПРЯМЫЕ
ОДНОКРАТНЫЕ
Оценивание погрешностей и неопределенности
результата измерений
1 РАЗРАБОТАНЫ Федеральным государственным унитарным предприятием Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева Госстандарта России (ФГУП ВНИИМ им. Д.И. Менделеева)
ВНЕСЕНЫ Управлением метрологии Госстандарта России
2 УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 октября 2004 г. № 43-ст
3 ВЗАМЕН МИ 1552-86
РЕКОМЕНДАЦИИ ПО МЕТРОЛОГИИ
Государственная система обеспечения единства измерений
ИЗМЕРЕНИЯ ПРЯМЫЕ ОДНОКРАТНЫЕ
Оценивание погрешностей и неопределенности результата измерений
State system for ensuring the uniformity of measurements.
Direct single measurements. Estimation of errors and uncertainty of measurements result
Дата введения 2005-01-01
1 Область применения
Настоящие рекомендации распространяются на нормативные, конструкторские, технические и другие документы, устанавливающие методики выполнения измерений (МВИ), и содержат методы оценивания характеристик погрешности и неопределенности результатов прямых однократных измерений. Разрабатываемые МВИ должны соответствовать требованиям ГОСТ Р 8.563.
Пример оценивания погрешности однократного измерения приведен в приложении А.
2 Нормативные ссылки
В настоящих рекомендациях использованы ссылки на следующие нормативные документы:
ГОСТ 8.207-76 Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения
ГОСТ 8711-93 ( МЭК 51-2-84) Приборы аналоговые показывающие электроизмерительные прямого действия и вспомогательные части к ним. Часть 2. Особые требования к амперметрам и вольтметрам
ГОСТ Р 8.563-96 Государственная система обеспечения единства измерений. Методики выполнения измерений
РМГ 43-2001 Государственная система обеспечения единства измерений. Применение «Руководства по выражению неопределенности измерений»
РД 50-453-84 Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчета
МИ 1317-86 Государственная система обеспечения единства измерений. Результаты и характеристики погрешности измерений. Формы представления. Способы использования при испытаниях образцов продукции и контроле их параметров
3 Термины, определения, обозначения и сокращения
3.1 В настоящих рекомендациях применяют следующие термины с соответствующими определениями:
границы неисключенной систематической погрешности измерений: Границы интервала, внутри которого находится неисключенная систематическая погрешность измерений.
однократное измерение: Измерение, выполненное один раз.
неопределенность (измерений): Параметр, связанный с результатом измерений и характеризующий рассеяние значений, которые могли бы быть обоснованно приписаны измеряемой величине (по РМГ 43).
стандартная неопределенность и (измерений): Неопределенность результата измерений, выраженная в виде среднего квадратического отклонения (по РМГ 43).
1 Стандартную неопределенность, оцениваемую по типу А, uA вычисляют по формуле
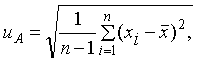
2 Стандартную неопределенность, оцениваемую по типу В, uB вычисляют по формуле
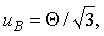
суммарная стандартная неопределенность uc (измерений): Стандартная неопределенность ре зультата измерений, равная положительному квадратному корню суммы дисперсий (по РМГ 43).
расширенная неопределенность U (измерений): Границы интервала, в пределах которого нахо дится большая часть распределения значений, которые могли бы быть приписаны измеряемой величине.
3.2 В настоящих рекомендациях использованы следующие сокращения:
3.3 В настоящих рекомендациях использованы следующие обозначения:
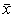
U — расширенная неопределенность;
U (Р) — расширенная неопределенность для уровня доверия Р;
S (Ã) — СКО случайной погрешности результата измерений;
zP /2 — квантиль нормального распределения для доверительной вероятности Р ;
Θ(Р) — доверительные границы систематической погрешности измерения для доверительной вероятности Р ;
т — число суммируемых НСП;
4 Общие положения
4.1 За результат однократного измерения Ã принимают значение величины, полученное при измерении.
4.2 На этапе перехода от погрешности к неопределенности целесообразно указывать характеристики и погрешности, и неопределенности результата измерения.
Составляющие погрешности результата измерения должны быть известны до проведения измерения. Предполагают, что известные систематические погрешности исключены (внесены поправки на все известные источники неопределенности, имеющие систематический характер).
4.3 Полагают, что распределение случайных погрешностей не противоречит нормальному распределению, а неисключенные систематические погрешности, представленные заданными границами ±Θ, распределены равномерно.
В целях количественного выражения неопределенности результата измерения, представленной в виде границ отклонения значения величины от ее оценки [- Θ; + Θ] (неполное знание о значении величины), полагают, что распределение возможных значений измеряемой величины в указанных границах не противоречит равномерному распределению.
4.4 Выполнение однократных измерений обосновывают следующими факторами:
— производственной необходимостью (разрушение образца, невозможность повторения измерения, экономическая целесообразность и т.д.);
— возможностью пренебрежения случайными погрешностями;
— случайные погрешности существенны, но доверительная граница погрешности результата измерения не превышает допускаемой погрешности измерений;
— стандартная неопределенность, оцениваемая по типу А, существенна, но расширенная неопределенность не превышает заданного предела.
1 Случайные погрешности считают пренебрежимо малыми по сравнению с неисключенными систематическими, если
S( Ã) — СКО случайных погрешностей результата измерения.
2 Неопределенность, оцениваемую по типу А, считают пренебрежимо малой по сравнению с неопределенностью, оцениваемой по типу В, если выполняется условие
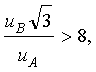
4.5 При определении доверительных границ погрешности или расширенной неопределенности для уровня доверия Р результата измерения принимают вероятность, равную 0,95.
В особых случаях, например при измерениях, которые нельзя повторить, допускается указывать доверительные границы или расширенную неопределенность для уровня доверия Р и более высоких вероятностей.
4.6 При вычислениях следует пользоваться правилами округления в соответствии с МИ 1317. Доверительные границы погрешности (характеристики погрешности) и расширенная неопределенность (расширенная неопределенность для уровня доверия Р) результата измерения должны быть представлены не более чем двумя значащими цифрами.
5 Составляющие погрешности и неопределенности результата измерения
5.1 Составляющими погрешности результата однократного измерения являются погрешности СИ, метода, оператора, а также погрешности, обусловленные изменением условий измерения.
5.2 Погрешность результата однократного измерения чаще всего представлена НСП и случайными погрешностями.
Неопределенность результата однократного измерения может быть представлена стандартными неопределенностями, оцениваемыми по типам А и В.
5.3 Характеристикой НСП могут быть:
5.4 Характеристикой случайных погрешностей могут быть:
— доверительные границы ± e (Р).
5.5 Погрешность СИ определяют на основании их метрологических характеристик, которые должны быть указаны в нормативных и технических документах, и в соответствии с РД 50-453.
5.6 Погрешности метода и оператора должны быть определены при разработке и аттестации конкретной МВИ.
6 Оценивание неисключенной систематической погрешности и стандартной неопределенности, оцениваемой по типу В, результата измерения
6.1 НСП результата измерения выражают границами этой погрешности, если среди составляющих погрешности результата измерения в наличии одна НСП.
6.2 Доверительные границы НСП результата измерения вычисляют следующим образом.
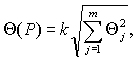
При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.
При доверительной вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если число суммируемых составляющих т > 4. Если же число составляющих равно четырем (т = 4), то поправочный коэффициент k ≈ 1,4; при т = 3 k ≈ 1,3; при т = 2 k ≈ 1,2. Более точное значение k для доверительной вероятности Р = 0,99 при числе составляющих т £ 4 в зависимости от соотношения составляющих l определяют по графику [ k = f ( m , l )] в соответствии с требованиями ГОСТ 8.207.
При условии, указанном в 6.2.1, суммарную стандартную неопределенность, оцениваемую по типу В, ис, B вычисляют по формуле
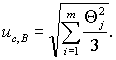
6.2.2 При наличии нескольких НСП, заданных доверительными границами Θ j (Р i ), рассчитанными по формуле ( 5), доверительную границу НСП результата однократного измерения вычисляют по формуле
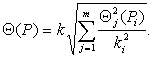
При условии, указанном выше, суммарную стандартную неопределенность, оцениваемую по типу В, вычисляют по формуле
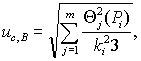
Значения коэффициентов k и ki определяют в соответствии с требованиями 6.2.1.
7 Оценивание случайной погрешности и стандартной неопределенности, оцениваемой по типу А, результата измерения
7.1 Доверительные границы случайной погрешности и стандартную неопределенность, оцениваемую по типу А, результата измерения вычисляют следующим образом.
7.1.1 Если случайные погрешности представлены несколькими СКО Si , то СКО результата однократного измерения S( Ã) вычисляют по формуле
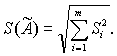
Учитывая условия 7.1.1, стандартную неопределенность, оцениваемую по типу А, результата однократного измерения и A вычисляют по формуле
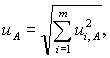

Доверительную границу случайной погрешности результата измерения e (Р) вычисляют по формуле
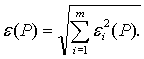
7.1.3 Если случайные погрешности представлены доверительными границами, соответствующими разным вероятностям, сначала определяют СКО результата измерения по формуле
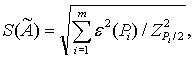
а затем вычисляют доверительные границы случайной погрешности результата измерения по формуле ( 11).
8 Оценивание погрешности и расширенной неопределенности результата измерения
8.1 Если погрешности метода и оператора пренебрежимо малы по сравнению с погрешностью используемых СИ (не превышают 15 % погрешности СИ), то за погрешность результата измерения принимают погрешность используемых СИ.
Расширенную неопределенность для уровня доверия Р вычисляют по формуле
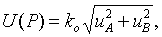
9 Форма представления результата измерения
9.1 Форма представления результатов однократных измерений должна соответствовать МИ 1317.
9.2 При симметричной доверительной погрешности результат однократного измерения представляют в форме Ã; ± D (Р); Р или Ã; ± D (Р), или Ã; U (Р).
Значение результата измерения должно оканчиваться цифрами того же разряда, что и значение погрешности или расширенной неопределенности для уровня доверия.
ПРИЛОЖЕНИЕ А
(справочное)
Расчет погрешности измерения напряжения показывающим прибором
Однократное измерение напряжения на участке электрической цепи сопротивлением R = 4 Ом.
А.1 Априорные данные об исследуемом объекте
Для измерения выбирают вольтметр класса точности 0,5 по ГОСТ 8711 (приведенная погрешность 0,5 %) с верхним пределом диапазона измерений U п p = 1,5 В. Вольтметр имеет магнитный экран. Некоторый запас по точности средства измерений необходим из-за возможного наличия дополнительных погрешностей, погрешности метода и т.д.
Инструментальная составляющая погрешности определяется основной и дополнительной погрешностями.
Основная погрешность прибора указана в приведенной форме. Следовательно, предел допускаемой основной погрешности вольтметра
Дополнительная погрешность из-за влияния магнитного поля не превышает 1,5 % нормирующего значения прибора и равна ±0,0225 В (0,015 · 1,5). Дополнительная температурная погрешность, обусловленная отклонением температуры от нормальной (20 °С) на 10 °С, не превышает 60 % предела допускаемой основной погрешности, эта дополнительная погрешность равна ±0,0045 В (0,0075 · 0,6).
А.2 Оценивание погрешности результата измерения
Погрешность метода определяется соотношением между сопротивлением участка цепи R и сопротивлением вольтметра RV . Сопротивление вольтметра известно: RV = 1000 Ом. При подсоединении вольтметра к цепи исходное напряжение Ux изменяется на
Отсюда методическая погрешность D M в абсолютной форме
Методическая погрешность δм в относительной форме
Оцененная методическая погрешность является систематической составляющей погрешности измерений и должна быть внесена в результат измерения в виде поправки 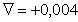
à = 0,90 + 0,004 = 0,904 В.
Находят границы погрешности результата измерения.
Поскольку основная погрешность применяемого средства измерений и его дополнительные погрешности заданы границами, следует рассматривать эти погрешности как неисключенные систематические. Воспользовавшись формулой ( 5), находят доверительную границу неисключенной систематической погрешности результата измерения при доверительной вероятности Р = 0,95:
Результат измерения в соответствии с разделом 9 следует представить в форме
à = 0,904 В; D (Р) = ±0,027 В; Р = 0,95 или (0,904 ± 0,027) В; Р = 0,95.
Ключевые слова: результат измерения, однократные измерения, среднее квадратическое отклонение, стандартная неопределенность, оцениваемая по типу А и по типу В, доверительная погрешность, расширенная неопределенность, коэффициент охвата, неисключенная систематическая погрешность