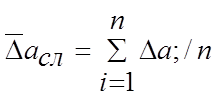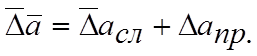Что принимают за абсолютную ошибку для табличных и универсальных постоянных величин

Абсолютная погрешность и ее граница

Вычислительная математика. Абсолютная погрешность

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ И ЕЕ ГРАНИЦА.

ЗАПИСЬ ПРИБЛИЖЕННОГО ЧИСЛА.

ВЕРНЫЕ И ЗНАЧАЩИЕ ЦИФРЫ ЧИСЛА

а – приближенное число

Разность х – а между точным числом х и приближенным числом а называется погрешностью приближения.

Модуль погрешности называется абсолютной погрешностью и обозначается ∆:

Погрешность и абсолютная погрешность имеют ту же размерность, что и рассматриваемая величина

Граница абсолютной погрешности ∆а – положительное число, которое больше или равно абсолютной погрешности или:

Если задана граница абсолютной погрешности ∆а, то число а есть приближенное значение числа х с точностью до ∆а и записывают

х = а ± ∆а, например: 94,5 ± 0,3

В отличие от абсолютной погрешности, граница абсолютной погрешности не определяется однозначно, поэтому на практике выбирается такое значение границы абсолютной погрешности, которое удобно для вычислений и обеспечивает максимальную точность.

Цифра приближенного числа а, записанного в виде десятичной дроби, называется верной (точной), если граница абсолютной погрешности числа не превышает (меньше или равно) единицы того разряда, в котором стоит эта цифра. В противном случае она называется сомнительной, например:

цифру 5, разряд единицы, единица разряда 1 и 0,2

Цифра 6, разряд десятые, единица разряда 0,1 и 0,2 > 0,1 (граница погрешности превышает единицу разряда), значит цифра 6 – сомнительная. Значит и цифра 3 (сотые) будет также сомнительной

2 и 5 – верные цифры, 6 и 3 – сомнительные цифры числа

Запись чисел с сохранением только верных цифр широко используется во всех математических таблицах, в справочниках (физика, астрономия, техника). При этом, по записи приближенного числа можно оценить погрешность приближения, например:

табличные данные: температура кипения золота – 2700 ºС, значит граница абсолютной погрешности 1 ºС, температура кипения йода – 182,8 ºС, значит граница абсолютной погрешности 0,1 ºС.

Записи приближенных чисел 0,3; 0,30; 0,300 – неравносильны, т.к. приближенное число 0,3 имеет погрешность не более 0,1;

приближенное число 0,30 имеет погрешность не более 0,01;

приближенное число 0,300 имеет погрешность не более 0,001.

В записи приближенных чисел принято соблюдать следующие правила:

Записать правильно следующие приближенные числа:

а = 0,3500 (последние верные цифры нули)

В некоторых заданиях необходимо наоборот определить абсолютную погрешность по записи приближенного числа, например,

Указать абсолютную погрешность приближенных чисел:

Число в стандартном виде записывают так:

показатель m – называется порядком числа.

Если число, записанное в виде десятичной дроби содержит все верные цифры, то все его цифры, начиная с первой слева отличной от нуля, называют значащими, например:

7,03 – три значащие цифры

4400 – четыре значащие цифры

0,000270 – три значащие цифры (нули, расположенные левее первой, отличной от нуля цифры, не считаются значащими 0,000270).

Округление числа – это замена его числом с меньшим количеством значащих цифр. При округлении числа до m значащих цифр отбрасывают все цифры, стоящие правее m-ой значащей цифры, заменяя их на нули (при сохранении разряда). При этом, если первая из отбрасываемых цифр ≥ 5, то последнюю оставшуюся цифру увеличивают на единицу,

Округлить число с заданной точностью:

Значащие цифры – 1, 5, 7 и 8, цифра 3 – сомнительная, т.к. 0,001 > 0,0001 (единицы разряда)

1,5783 ≈ 1,578 (последняя из отбрасываемых цифр 3

Значащие цифры – 2, 3, 4, 9 и 9, цифра 7 – сомнительная

7>5, значит предыдущую увеличиваем на 1, получим

159734 ≈ 160000 = 160·10 3

28,34 ≈ 0 – ни одна из цифр не является значащей 1000 > 10, т.к. задана точность 1000, а заданное число меньше, чем погрешность.

Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие)

Источник

1. Совокупность и измеренных значений величины а заносят в таблицу измерений.

2. Находится среднее значение величины

.

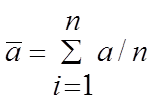
3. Определяются абсолютные погрешности отдельных измерений и заносятся в таблицу

.

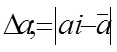
Находится случайная средняя погрешность

и записывается в таблицу.

5. Определяется как сумма средней и приборной погрешностей средняя погрешность многократно измеряемой величины

в) Погрешности косвенно измеряемых величин.

Пусть искомая величина у является функцией m непосредственно измеряемых величин Х₁, Х₂…Х_m, для

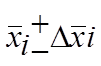
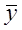
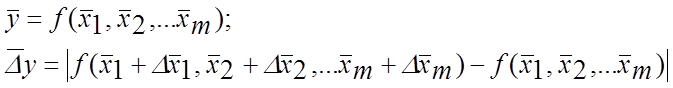
каждой из которых известно среднее значение и погрешность т.е. . Тогда для среднего значения функции и погрешности по определению имеем:

(10)

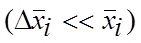
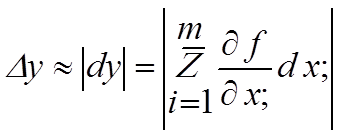
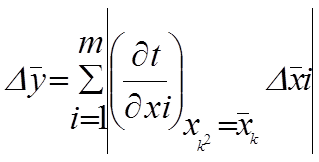
т.е. абсолютная погрешность на языке математики представляет собой модуль приращения функции при приращении аргументов. Учитывая малость погрешностей по сравнению с результатом , а также известную из математики теорему о дифференциале как главной линейной части приращения функции, можно ( с точностью до членов второго по Δх_i ) приращение Δу приближенно заменить дифференциалом.

,

. (11)

Для относительной погрешности соответственно имеем:

. (12)

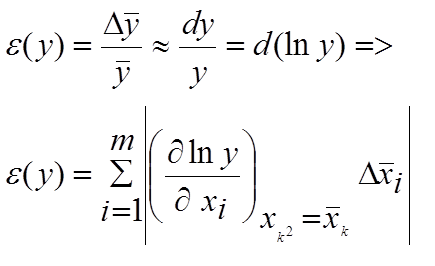
Формулы (11), (12) являются исходными для вычисления погрешностей любых косвенно измеряемых величин.

Когда косвенно измеряемая величина представляет собой произведение или степени непосредственно измеряемых величин, тогда целесообразнее вначале найти относительную погрешность по формуле (12), а через неё найти абсолютную.

Например при определении плотности тела цилиндрической формы используется формула

, (13)

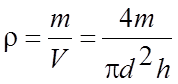
где m – масса, d – диаметр, h – высота непосредственно измеряемые величины, для которых в результате измерений найдены их средние значения и погрешности

,

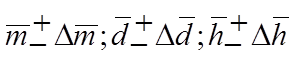
Т.к. плотность выражается через произведение и степени непосредственно измеряемых величин, будем вначале находить относительную погрешность. Из (13) имеем

.

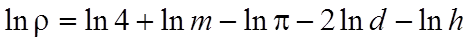
Находим частные производные (lnρ) но m, d, h, π (здесь учитываем что постоянная π также имеет погрешность см. погрешности табличных величин)

,

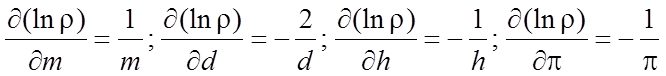
подставляя производные в формулу (12), получаем

, (14)

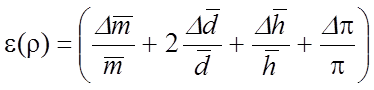
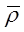
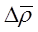
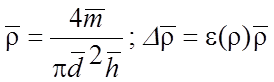
соответственно для и получим:

. (15)

5. Правила округления и согласования результатов измерений.

После проведения измерений и вычислений не менее важно грамотно округлить и записать конечный результат. Для этого существуют следующие правила.

1) Все промежуточные измерения и вычисления делаются с точностью не менее n значащих цифр.

(Точность измерений – n заранее определятся целями эксперимента – научными, учебными и т. д. Мы в учебных целях будем ограничиваться тремя значащими цифрами).

2) Вначале округляется абсолютная погрешность до первой значащей цифры если она больше, равна трём, либо до двух значащих цифр в противном случае.

3) После округления погрешности округляется сам результат таким образом, чтобы последние порядки результата и погрешности совпадали.

Пример; пусть в результате измерения плотности и ускорения свободного падения получены значения:

а) ; ,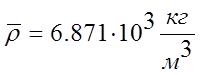

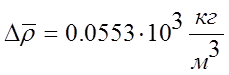
б) ; ,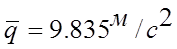

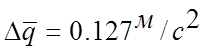
округляя в соответствии с правилами, имеем:

а) ; ,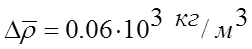

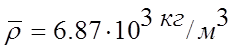
б) ; ,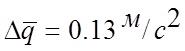

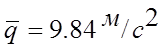
окончательная запись результата:

а) ;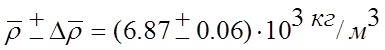

б) .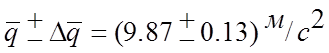

6. Порядок выполнения лабораторных работ и оформление отчёта.

Выполнение каждой лабораторной работы проводится по следующей схеме.

1. Познакомится по учебникам или лекциям с теорией соответствующей работы и внимательно изучить описание лабораторной работы.

2. Познакомится с лабораторной установкой, входящими в неё измерительными приборами, изучить последовательность выполнения работы.

3. Аккуратно произвести измерения согласно рекомендациям в описании работы и записать результаты в таблицу измерений. Выписать дополнительные данные необходимые для расчётов.

4. Обработка результатов измерений, расчёт искомых величин и их погрешностей. Протокол измерений и вычислений в черновом варианте представляется преподавателю для проверки.

5. Оформление отчёта о выполненной лабораторной работе (ниже указан порядок оформления отчёта).

6. Защита лабораторной работы

— сдача оформленного отчёта

— ответа на теоретические вопросы по теме работы.

Порядок оформления отчёта.

Отчёт представляется на двойном листе.

На титульной странице записывается полное название лабораторной работы; её номер в методических указаниях; Ф.И.О. студента выполнившего работу; факультет, форма обучения и номер группы.

На внутренних страницах двойного листа производят записи в следующей последовательности.

1. Цель работы: (указана в описании работы)

2. Приборы и материалы: (также указаны в описании. Здесь перечисляются, а на измерительные приборы составляется приборная таблица, где даётся краткая характеристика приборов.

Например; приборная таблица лабораторной работы №1.

Источник

Погрешности измерений, представление результатов эксперимента

п.1. Шкала измерительного прибора

Примеры шкал различных приборов:

Манометр – прибор для измерения давления, круговая шкала

Вольтметр – прибор для измерения напряжения, дуговая шкала

Индикатор громкости звука, линейная шкала

п.2. Цена деления

Пример определения цены деления:

Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления.

Цена деления: \begin \triangle=\frac\\ \triangle=\frac<10-5><24+1>=\frac15=0,2\ c \end

п.3. Виды измерений

Физическую величину измеряют с помощью прибора

Измерение длины бруска линейкой

Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений

Определение площади столешницы при измеренной длине и ширине

п.4. Погрешность измерений, абсолютная и относительная погрешность

Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)

Определяется несовершенством методов и допущениями в методике.

Погрешность теории (модели)

Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.

Определяется субъективным фактором, ошибками экспериментатора.

Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.

В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:

Пример получения результатов прямых измерений с помощью линейки:

Второе измерение точнее, т.к. его относительная погрешность меньше.

п.5. Абсолютная погрешность серии измерений

Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).

Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.

Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.

Составим расчетную таблицу:

Сначала находим среднее значение всех измерений: \begin m_0=\frac<99,8+101,2+100,3><3>=\frac<301,3><3>\approx 100,4\ \text <г>\end Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin \triangle_1=|100,4-99,8|=0,6\\ \triangle_2=|100,4-101,2|=0,8\\ \triangle_3=|100,4-100,3|=0,1 \end Находим среднее абсолютное отклонение: \begin \triangle_=\frac<0,6+0,8+0,1><3>=\frac<1,5><3>=0,5\ \text <(г)>\end Мы видим, что полученное значение \(\triangle_\) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: \begin \triangle m=max\left\<\triangle_; d\right\>=max\left\<0,5; 0,05\right\>\ \text <(г)>\end Записываем результат: \begin m=m_0\pm\triangle m\\ m=(100,4\pm 0,5)\ \text <(г)>\end Относительная погрешность (с двумя значащими цифрами): \begin \delta_m=\frac<0,5><100,4>\cdot 100\text<%>\approx 0,050\text <%>\end

п.6. Представление результатов эксперимента

Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.

Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.

п.7. Задачи

Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?

Составим таблицу для расчета цены деления:

Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):

Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.

Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка

Мерой точности является относительная погрешность измерений. Получаем: \begin \delta_1=\frac<0,1><4,0>\cdot 100\text<%>=2,5\text<%>\\ \delta_2=\frac<0,03><4,0>\cdot 100\text<%>=0,75\text <%>\end Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.

Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.

Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.

Источник

Что принимают за абсолютную ошибку для табличных и универсальных постоянных величин

Числовой интервал 2Δx, в котором с вероятностью, близкой к единице, содержится истинное значение величины x, называется доверительным интервалом. Относительная noгрешность ε_x — безразмерная величина, равная отношению абсолютной погрешности, измеренному значению величины ε_x = Δx/x.

2. Статистическая обработка результатов измерений

2.1. Вычисление погрешностей прямых измерений
При оценке точности прямого измерения будем учитывать случайую прогрешность и погрешность средства измерения.

Слепень разброса результатов измерения и случайную погрешность можно оценить по величине среднего отклонения результатов от среднего значения:

2.1.2. Погрешности средств измерений (приборная погрешность)
Погрешность средства измерения Δx_пр — разность между показанием прибора и истинным значением измеряемой величины.
Погрешность средства измерения является систематической, то есть даёт отклонение измеренной величины от истинной в одну сторону, но мы никогда не знаем, в какую именно. Любой прибор позволяет проводить измерения лишь с определенной точностью, погрешность зависит от вида прибора.
1. В приборах, у которых переход от одного значения к другому осуществляется скачком (стрелочный секундомер, весы с разновесами), инструментальная погрешность равна величине скачка.
2. Инструментальная погрешность приборов, снабженных нониусом (штангенциркуль, микрометр), равна точности нониуса:

3. Погрешности электроизмерительных стрелочных приборов рассчитываются по классу точности.
Класс точности К определен отношением абсолютной погрешности Δx к используемому пределу измерения прибора X и выражен в процентах.

К = Δx/X ·100%,

Следовательно, абсолютная погрешность измерения данным прибором рассчитывается по формуле:

Δx = КX/100% (5)

Электроизмерительные приборы имеют восемь классов точности: К = (0.05; 0.1: 0.2: 0,5: 1,0: 1,5: 2.5; 4.0). Чем выше класс точности, тем меньше значение К и меньше погрешность измерения.
4. Погрешность измерения цифровыми приборами рассчитывается по формулам, представленным в паспорте прибора. Так для микро-мультиметра «Электроника ММЦ-01» формула для расчета относительной погрешности измерения напряжения постоянного тока, выраженной в процентах, имеет вид:

5. Для прочих приборов с делениями (линейка, транспортир термометр и т. п.) в качестве инструментальной погрешности принимается погрешность отсчёта, равная половине цены деления шкалы прибора.

2.1.3. Полная погрешность прямых измерений
Результирующая погрешность прямого измерения рассчитывается по формуле:
Δx_прям = Δx_пр + Δx_сл (7)

Если Δx_пр >> Δx_сл, то Δx_прям ≈ Δx_пр(7а)

В случае, если Δx_сл>>Δx_пр, погрешностью средства измерений можно пренебречь. Однако, это одновременно говорит о том, что эксперимент проведен некачественно. Необходимо увеличить число измерений, чтобы уменьшить случайную погрешность.
Если данная физическая величина измеряется один раз, то в качестве погрешности прямого измерения берут инструментальную погрешность Δx_пр.
Значение результата прямых измерений записывается в виде x = x_ср±Δx (8)

2.2. Погрешность физических постоянных, табличных данных, данных установок (погрешности округления)
Физические постоянные (константы) считают точными величинами. В этом случае значение данной величины подставляется в расчетную формулу с числом значащих цифр на одну больше, чем число значащих цифр, полученных в результате прямых измерений. При этом относительная погрешность округления константы окажется на порядок меньше погрешности прямого измерения и ею можно пренебречь.
Многие табличные данные, используемые в расчетах, представлены с большой точностью. В этом случае при выборе числа значащих цифр для подстановки в расчетную формулу руководствуются предыдущим правилом.
Если же табличные данные, данные установок определены с точностью, сопоставимой с результатом прямых измерений, то такие данные считаются приближенными. В этом случае погрешность табличной величины принимают равной половине единицы последнего разряда, приведенного в таблице числа.
Пример: если m = 8,0 г, то Δm = 0,05 г;
если М = 4 г, то ΔМ = 0,5 г.
Результатом косвенных измерений является величина Y, рассчитанная по соответствующей формуле с использованием средних значений результатов прямых измерений.
Погрешность косвенно измеряемой величины определяется погрешностями величин, полученных в процессе прямых измерений, а также погрешностями табличных данных и других постоянных, входящих в расчетную формулу.
Формула для вычисления относительной погрешности косвенного измерения ε_Y = ΔY/Y зависит от вида расчётной формулы для Y и приводится в описании каждой лабораторной работы. Абсолютная погрешность косвенного измерения ΔY очевидно может быть рассчитана по формуле:
ΔY = Y·ε_Y (9)

2.2. Правило округления абсолютной погрешности.
Количество значащих цифр абсолютной погрешности не должно быть более двух. Две цифры оставляют в том случае, если первая значащая цифра погрешности «1» или «2». Если первая цифра больше «2», то абсолютную погрешность округляют так, чтобы оставалась одна значащая цифра.

Источник