Чем меньше уровень значимости
4. Уровень значимости
Уровни статистической значимости
Уровень значимости – это вероятность того, что мы сочли различия существенными, в то время как они на самом деле случайны.
Итак, уровень значимости имеет дело с вероятностью.
Уровень значимости показывает степень достоверности выявленных различий между выборками, т.е. показывает, насколько мы можем доверять тому, что различия действительно есть.
Современные научные исследования требуют обязательных расчётов уровня статистической значимости результатов.
Обычно в прикладной статистике используют 3 уровня значимости.
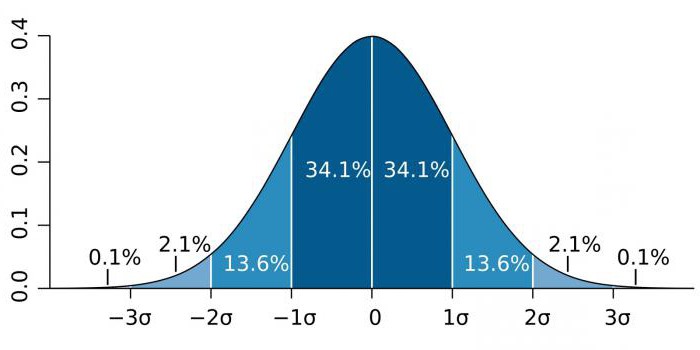
Это 5%-ный уровень значимости. До 5% составляет вероятность того, что мы ошибочно сделали вывод о том, что различия достоверны, в то время как они недостоверны на самом деле. Можно сказать и по-другому: мы лишь на 95% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,95. Общий смысл критерия останется тем же.
Это 1%-ный уровень значимости. Вероятность ошибочного вывода о том, что различия достоверны, составляет не более 1%. Можно сказать и по-другому: мы на 99% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,99. Смысл останется тем же.
Это 0,1%-ный уровень значимости. Всего 0,1% составляет вероятность того, что мы сделали ошибочный вывод о том, что различия достоверны. Это — самый надёжный вариант вывода о достоверности различий. Можно сказать и по-другому: мы на 99,9% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,999. Смысл опять-таки останется тем же.
Уровень значимости – это допустимая ошибка в нашем утверждении, в нашем выводе.
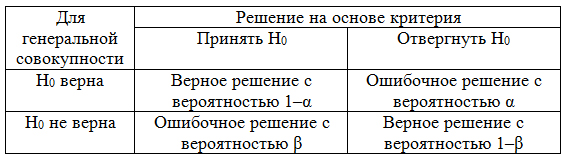
Возможны ошибки двух родов: первого рода ( α ) и второго рода ( β ).
Ошибка I рода – мы отклонили нулевую гипотезу, в то время как она верна.
Вероятность того, что принято правильное решение: 1 – α = 0,95, или 95%.
Уровни значимости для ошибок I рода
1. α ≤ 0,05 – низший уровень
Низший уровень значимости – позволяет отклонять нулевую гипотезу, но еще не разрешает принять альтернативную.
2. α ≤ 0,01 – достаточный уровень
Достаточный уровень – позволяет отклонять нулевую гипотезу и принимать альтернативную.
G – критерий знаков
T – критерий Вилкоксона
U – критерий Манна – Уитни.
Для них обратное соотношение.
3. α ≤ 0,001 – высший уровень значимости.
На практике различия считают достоверными при р ≤ 0,05.
Для ненаправленной статистической гипотезы используется двусторонний критерий значимости. Он более строгий, так как проверяет различия в обе стороны: в сторону нулевой гипотезы и в сторону альтернативной. Поэтому для него используется критерий значимости 0,01.
Мощность критерия – его способность выявлять даже мелкие различия если они есть. Чем мощнее критерий, тем лучше он отвергает нулевую гипотезу и подтверждает альтернативную.
Здесь появляется понятие: ошибка II рода.
Ошибка II рода – это принятие нулевой гипотезы, хотя она не верна.
Мощность критерия: 1 – β
Чем мощнее критерий, тем он привлекательнее для исследователя. Он лучше отвергает нулевую гипотезу.
Чем привлекательны маломощные критерии?
Достоинства маломощных критериев
Широкий диапазон, по отношению к самым разным данным
Применимость к неравным по объему выборкам.
Большая информативность результатов.
Второй по популярности — критерий хи-квадрат, χ 2
Т-критерий Стьюдента – это частный случай дисперсионного анализа для более маленькой по объёму выборки.
Уровень значимости в статистике
Уровень значимости в статистике является важным показателем, отражающим степень уверенности в точности, истинности полученных (прогнозируемых) данных. Понятие широко применяется в различных сферах: от проведения социологических исследований, до статистического тестирования научных гипотез.
Определение
Уровень статистической значимости (или статистически значимый результат) показывает, какова вероятность случайного возникновения исследуемых показателей. Общая статистическая значимость явления выражается коэффициентом р-value (p-уровень). В любом эксперименте или наблюдении существует вероятность, что полученные данные возникли из-за ошибок выборки. Особенно это актуально для социологии.
То есть статистически значимой является величина, чья вероятность случайного возникновения крайне мала либо стремится к крайности. Крайностью в этом контексте считают степень отклонения статистики от нуль-гипотезы (гипотезы, которую проверяют на согласованность с полученными выборочными данными). В научной практике уровень значимости выбирается перед сбором данных и, как правило, его коэффициент составляет 0,05 (5 %). Для систем, где крайне важны точные значения, этот показатель может составлять 0,01 (1 %) и менее.
История вопроса
Понятие уровня значимости было введено британским статистиком и генетиком Рональдом Фишером в 1925 году, когда он разрабатывал методику проверки статистических гипотез. При анализе какого-либо процесса существует определенная вероятность тех либо иных явлений. Трудности возникают при работе с небольшими (либо не очевидными) процентами вероятностей, подпадающими под понятие «погрешность измерений».
При работе со статистическими данными, недостаточно конкретными, чтобы их проверить, ученые сталкивались с проблемой нулевой гипотезы, которая «мешает» оперировать малыми величинами. Фишер предложил для таких систем определить вероятность событий в 5 % (0,05) в качестве удобного выборочного среза, позволяющего отклонить нуль-гипотезу при расчетах.
Введение фиксированного коэффициента
В 1933 году ученые Ежи Нейман и Эгон Пирсон в своих работах рекомендовали заранее (до сбора данных) устанавливать определенный уровень значимости. Примеры использования этих правил хорошо видны во время проведения выборов. Предположим, есть два кандидата, один из которых очень популярен, а второй – малоизвестен. Очевидно, что первый кандидат выборы выиграет, а шансы второго стремятся к нулю. Стремятся – но не равны: всегда есть вероятность форс-мажорных обстоятельств, сенсационной информации, неожиданных решений, которые могут изменить прогнозируемые результаты выборов.
Нейман и Пирсон согласились, что предложенный Фишером уровень значимости 0,05 (обозначаемый символом α) наиболее удобен. Однако сам Фишер в 1956 году выступил против фиксации этого значения. Он считал, что уровень α должен устанавливаться в соответствии с конкретными обстоятельствами. Например, в физике частиц он составляет 0,01.
Значение p-уровня
Термин р-value впервые использован в работах Браунли в 1960 году. P-уровень (p-значение) является показателем, находящимся в обратной зависимости от истинности результатов. Наивысший коэффициент р-value соответствует наименьшему уровню доверия к произведенной выборке зависимости между переменными.
Данное значение отражает вероятность ошибок, связанных с интерпретацией результатов. Предположим, p-уровень = 0,05 (1/20). Он показывает пятипроцентную вероятность того, что найденная в выборке связь между переменными – всего лишь случайная особенность проведенной выборки. То есть, если эта зависимость отсутствует, то при многократных подобных экспериментах в среднем в каждом двадцатом исследовании можно ожидать такую же либо большую зависимость между переменными. Часто p-уровень рассматривается в качестве «допустимой границы» уровня ошибок.
Кстати, р-value может не отражать реальную зависимость между переменными, а лишь показывает некое среднее значение в пределах допущений. В частности, окончательный анализ данных будет также зависеть от выбранных значений данного коэффициента. При p-уровне = 0,05 будут одни результаты, а при коэффициенте, равном 0,01, другие.
Проверка статистических гипотез
Уровень статистической значимости особенно важен при проверке выдвигаемых гипотез. Например, при расчетах двустороннего теста область отторжения разделяют поровну на обоих концах выборочного распределения (относительно нулевой координаты) и высчитывают истинность полученных данных.
Предположим, при мониторинге некоего процесса (явления) выяснилось, что новая статистическая информация свидетельствует о небольших изменениях относительно предыдущих значений. При этом расхождения в результатах малы, не очевидны, но важны для исследования. Перед специалистом встает дилемма: изменения реально происходят или это ошибки выборки (неточность измерений)?
Эффективность
Необходимо учитывать, что коэффициенты α и р-value не являются точными характеристиками. Каким бы ни был уровень значимости в статистике исследуемого явления, он не является безусловным основанием для принятия гипотезы. Например, чем меньше значение α, тем больше шанс, что устанавливаемая гипотеза значима. Однако существует риск ошибиться, что уменьшает статистическую мощность (значимость) исследования.
Исследователи, которые зацикливаются исключительно на статистически значимых результатах, могут получить ошибочные выводы. При этом перепроверить их работу затруднительно, так как ими применяются допущения (коими фактически и являются значения α и р-value). Поэтому рекомендуется всегда, наряду с вычислением статистической значимости, определять другой показатель – величину статистического эффекта. Величина эффекта – это количественная мера силы эффекта.
Уровень статистической значимости (р)
В таблицах результатов статистических расчётов в курсовых, дипломных и магистерских работах по психологии всегда присутствует показатель «р».
Например, в соответствии с задачами исследования были рассчитаны различия уровня осмысленности жизни у мальчиков и девочек подросткового возраста.
Уровень статистической значимости (p)
В правом столбце указано значение «р» и именно по его величине можно определить значимы различия осмысленности жизни в будущем у мальчиков и девочек или не значимы. Правило простое:
Откуда берется уровень статистической значимости «р»
Уровень статистической значимости вычисляется статистической программой вместе с расчётом статистического критерия. В этих программах можно также задать критическую границу уровня статистической значимости и соответствующие показатели будут выделяться программой.
Например, в программе STATISTICA при расчете корреляций можно установить границу «р», например, 0,05 и все статистически значимые взаимосвязи будут выделены красным цветом.
Если расчёт статистического критерия проводится вручную, то уровень значимости «р» выявляется путем сравнения значения полученного критерия с критическим значением.
Что показывает уровень статистической значимости «р»
Все статистические расчеты носят приблизительный характер. Уровень этой приблизительности и определяет «р». Уровень значимости записывается в виде десятичных дробей, например, 0,023 или 0,965. Если умножить такое число на 100, то получим показатель р в процентах: 2,3% и 96,5%. Эти проценты отражают вероятность ошибочности нашего предположения о взаимосвязи, например, между агрессивностью и тревожностью.
То есть, коэффициент корреляции 0,58 между агрессивностью и тревожностью получен при уровне статистической значимости 0,05 или вероятности ошибки 5%. Что это конкретно означает?
Выявленная нами корреляция означает, что в нашей выборке наблюдается такая закономерность: чем выше агрессивность, тем выше тревожность. То есть, если мы возьмем двух подростков, и у одного тревожность будет выше, чем у другого, то, зная о положительной корреляции, мы можем утверждать, что у этого подростка и агрессивность будет выше. Но так как в статистике все приблизительно, то, утверждая это, мы допускаем, что можем ошибиться, причем вероятность ошибки 5%. То есть, сделав 20 таких сравнений в этой группе подростков, мы можем 1 раз ошибиться с прогнозом об уровне агрессивности, зная тревожность.
Какой уровень статистической значимости лучше: 0,01 или 0,05
Уровень статистической значимости отражает вероятность ошибки. Следовательно, результат при р=0,01 более точный, чем при р=0,05.
В психологических исследованиях приняты два допустимых уровня статистической значимости результатов:
р=0,01 – высокая достоверность результата сравнительного анализа или анализа взаимосвязей;
р=0,05 – достаточная точность.
Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать
Проверка статистических гипотез
п.1. Понятие о статистической гипотезе
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| \(H_0\) | \(H_1\) | ||
| Принятая гипотеза | \(H_0\) | True Negative \(H_0\) принята верно | False Negative \(H_0\) принята неверно Ошибка 2-го рода |
| \(H_1\) | False Positive \(H_0\) отвергнута неверно \(H_1\) принята неверно Ошибка 1-го рода | True Positive \(H_0\) отвергнута верно \(H_1\) принята верно | |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Уровень значимости при проверке гипотезы
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости \(p\) | Решение о гипотезе \(H_0\) | Вывод для гипотезы \(H_1\) |
| \(p\gt 0,1\) | \(H_0\) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| \(0,5\lt p\leq 0,1\) | Истинность \(H_0\) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| \(0,01\lt p\leq 0,05\) | Отклонение \(H_0\), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| \(p\leq 0,01\) | Отклонение \(H_0\), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы \(H_1\).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с \(n\geq 100\) критический уровень снижают до α=0,01.
п.3. Критическая область
Различают 3 вида критических областей
п.4. Простая гипотеза и критерии согласия
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
\(H_0\): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
п.5. Критерий согласия \(X^2\) Пирсона
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| \(m_i\) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| \(f_i-m_i\) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| \(\frac<(f_i-m_i)^2> | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| \(m_i\) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| \(f_i-m_i\) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| \(\frac<(f_i-m_i)^2> | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(p_i\) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: \(X_e^2=36,84\)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для \(X_<кр>^2=X^2(\alpha,k-2)\).
Для уровня значимости α=0,05 и k=8, r=1 находим:
\(X_<кр>^2\approx 12,59\)
Получается, что: \(X_e^2\gt X_<кр>^2\)
Гипотеза \(H_0\) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x= <4;5;6;7>с редким числом попаданий:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 8 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 35 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(p_i\) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: \(X_e^2=1,12\)
Критическое значение статистики ищем в виде \(X_<кр>^2=X^2(\alpha,k-2)\), где α=0,05 и k=5, r=1
\(X_<кр>^2\approx 7,81\)
Получается, что: \(X_e^2\lt X_<кр>^2\)
Гипотеза \(H_0\) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики \(X_e^2\) в Примере 2, основной вклад внесло слагаемое для \(x_i=7\). Оно равно 34,34 и поэтому сумма \(X_e^2=36,84\) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты \(x_i=4,375\) слагаемое статистики равно 0,16 и сумма \(X_e^2=1,12\) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Выбор уровня значимости при проверке статистических гипотез
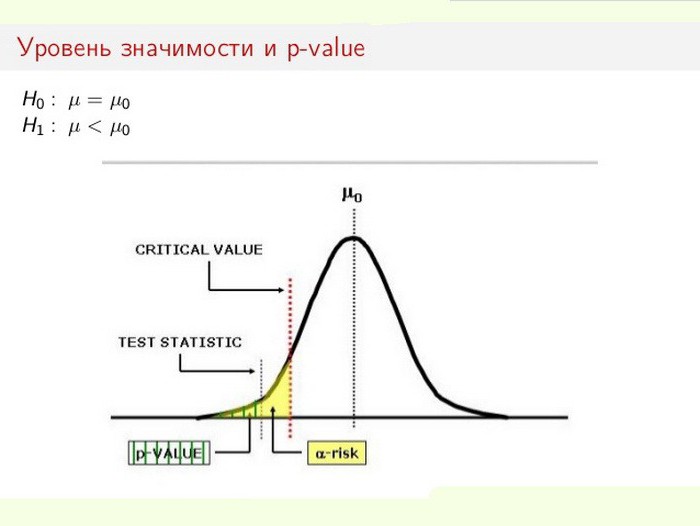
Проверка статистических гипотез основана на сравнении рассчитанного значения критерия с теоретическим значением, выбранного с заданным критическим уровнем значимости. От выбранного уровня значимости зависит результат проверки гипотез и сделанные исследователем выводы. Во многих учебниках и руководствах по использованию пакетов для статистического анализа приводится «магическое» значение 0,05, которое нужно выбирать в качестве критического уровня значимости. Можно ли всегда брать уровень значимости 0,05 или нет, попытаемся разобраться в этой статье.
Для начала кратко разберем основы проверки статистических гипотез. Статистической гипотезой будем называть любое предположение о законе распределения случайной величины или о параметрах этого закона. Это может быть предположение об отсутствии различий, об отсутствии взаимосвязи, о соответствии параметра заданному значению и т.д. Выделяют две виды гипотез: формулируемая гипотеза называется нулевой (основной) или гипотезой Н0. Также обязательно формулируют альтернативную (конкурирующую) гипотезу Н1. Предполагают, что либо верна гипотеза Н0 при ложной гипотезе Н1, либо вернаН1 при ложной гипотезеН0. Обе гипотезы одновременно быть ложными или истинными быть не могут.
Формулируют гипотезы таким образом, чтобы альтернативная гипотеза была «рабочей». Например, цель исследования доказать, что объем продаж увеличился на 10%. Тогда нулевая гипотеза будет сформулирована: объем продаж не увеличился. Цель проверки нулевой гипотезы будет заключаться в том, чтобы ее отвергнуть и доказать альтернативную гипотезу.
В зависимости от вида формулируемой нулевой гипотезы она может проверяться с помощью различных методов – статистических критериев. Статистический критерий – это некое правило, согласно которому нулевую гипотезу нужно принять или отвергнуть. Важно понимать, что при проверке гипотез мы работаем не с самой случайной величиной, а с данными выборки. Поэтому наши суждения на основе результатов проверки гипотез всегда имеют вероятностный характер. Какое бы решение мы не приняли, всегда существует ошибка принятия этого решения. Рассмотрим все возможные ошибки при принятии решений (см. таблицу).
Мы можем принять верную гипотезу Н0 или отвергнуть не верную гипотезу Н0 на основе критерия. В этом случае мы не совершаем никакой ошибки. А еще мы можем отвергнуть верную нулевую гипотезу – это называется ошибкой первого рода. Для оценки возможности совершения такой ошибки используют вероятность, обозначаемую α и называемую уровнем значимости критерия. Также возможна и ошибка второго рода β – когда мы принимаем неверную нулевую гипотезу. На практике может использоваться величина 1– β или мощность критерия – вероятность не совершить ошибку второго рода или принять неверную гипотезу.
Уровень значимости должен стремиться к нулю, а мощность критерия к 1. Эти два требования вступают в противоречие. Сделать равными нулю обе ошибки при проверке гипотез невозможно. С практической точки зрения обычно наиболее критической является ошибка первого рода, а не второго. И гипотеза Н0 формулируется так, чтобы задача была ее отвергнуть и доказать истинность Н1. В случае отвержения гипотезы нас интересует только ошибка первого рода. Поэтому критический уровень значимости задается исследователем, а уже мощность критерия можно посчитать по заданной вероятности ошибки первого рода. Исходя из заданного значения уровня значимости, берут теоретическое значение критерия по одной из таблиц распределения и сравнивают его с рассчитанным значением критерия. Именно в качестве такого критического значения предлагают брать уровень значимости 0,05.
В статистических пакетах обычно выдается не заданный нами уровень значимости, а накопленная вероятность наблюдения уровня статистического критерия (p-значение) при принятии нулевой гипотезы. Если p-величина меньше выбранного аналитиком критического уровня накопленной вероятности, то нулевая гипотеза отвергается. Чем меньше p-величина, тем меньше вероятность истинности нулевой гипотезы, тем сильнее основания отвергнуть нулевую гипотезу. Итак, выбор критического уровня имеет ключевое значение. Как же его выбрать?
При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости a. Однако при этом увеличивается вероятность ошибки второго рода b, т.е. снижается мощность критерия. Выбор уровня значимости требует компромисса между заданной значимостью и мощностью. Увеличивая уровень значимости, мы увеличиваем шансы отвергнуть нулевую гипотезу, что является нашей конечной целью, а с другой стороны мы также увеличиваем и вероятность ошибки первого рода.
При выборе критического уровня значимости необходимо обращать внимание на объем выборки. Общая идея тут следующая. При малом объеме выборки более вероятно получить случайный результат, например, получить различие в двух в выборках при их однородности. Следовательно, можно взять большую вероятность ошибки первого рода. При увеличении объема выборки случайные отклонения компенсируют друг друга, и получить значимое различие в выборках при их однородности менее вероятно. Следовательно, надо брать меньший уровень значимости. Стандартными уровнями значимости являются 0,1; 0,05; 0,01; 0,001. Поэтому нельзя всегда брать уровень значимость 0,05. Можно придерживаться следующих условных границ зависимости объема выборки от уровня значимости. Если объем выборки небольшой до 100 единиц, то можно вполне отвергнуть нулевую гипотезу при уровне значимости 0,05 или даже 0,1. При объеме выборки, измеряемой сотнями – от 100 до 1000, следует понизить уровень значимости хотя бы до 0,01. А при больших выборках, измеряемых тысячами наблюдений, уверенно отвергать нулевую гипотезу можно только при значимости меньшей 0,001.
Также при выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается важнее малого уровня значимости, и его значение выбирают относительно большим, например 0,1 или даже 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем последствия ошибок первого рода.
Кроме того, следует различать понятие статистической значимости и практической значимости. Заключение о практической значимости всегда делается исследователем, проверяющим гипотезу. И здесь истинными критерием является экспертное мнение исследователя, его опыт и интуиция, умение «чувствовать» истинный уровень значимости, а не применение стандартного значения 0,05. Окончательный выбор уровня значимости связан с риском, который наступает с выбором решения принимать или отвергать проверяемую гипотезу.