Что общего у фигур слева и чем отличаются справа петерсон

Математика 2 класс учебник Петерсон 1 часть — страница 29

Подготовили готовое домашнее задание к упражнениям на 29 странице по предмету математика за 2 класс. Ответы на задания: 7, 8, 9, 10, 11 и 12.

Учебник 1 часть — Страница 29.

В столовой за день израсходовали 40 кг хлеба. Из них за завтраком израсходовали 12 кг, за обедом – на 3 кг больше, чем за завтраком, а остальной хлеб израсходовали за ужином. Сколько хлеба израсходовали за ужином?

– Чтобы узнать, сколько килограммов хлеба израсходовали за ужином, надо из всей массы хлеба вычесть массу хлеба, которую израсходовали за завтраком и обедом. (Ищем часть.) Известно, что всего за день израсходовали 40 кг хлеба, а за завтраком 12 кг. Масса хлеба, которую израсходовали за обедом, не известна, но сказано, что она на 3 кг больше, чем за завтраком. Значит, мы можем ее найти, увеличив 12 кг на 3 кг. Затем сложим полученное число с 12 кг и найдем массу хлеба, которую израсходовали за завтраком и обедом. Вычтем ее из 40 кг и ответим на вопрос задачи.

1) 12 + 3 = 15 (кг) – израсходовали за обедом.
2) 12 + 15 = 27 (кг) – израсходовали за завтраком и обедом вместе.
3) 40 – 27 = 13 (кг)
Ответ: за ужином израсходовали 13 кг хлеба.

Какой отрезок короче и на сколько?

АВ = 12 см
CD = 7 см
Отрезок CD короче отрезка АВ
12 – 7 = 5 (см)
Ответ: отрезок CD короче отрезка АВ на 5 см.

Начерти в тетради треугольник ABC. Отметь внутри него точку D, а снаружи – точку Е. Проведи отрезок DE. Пересекает ли он стороны треугольника? Начерти отрезок MN, не пересекающий стороны треугольника. Где расположены его концы?

Отрезок DE, один конец которого расположен внутри, а другой – снаружи треугольника ABC, пересечет его сторону. Концы отрезка MN, не пересекающего сторон треугольника ABC, расположены либо оба снаружи, либо оба внутри этого треугольника.

Что общего у фигур слева и чем они отличаются от фигур справа?

Все фигуры слева – замкнутые линии, а справа – незамкнутые линии.

Найди устно сумму удобным способом: 2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18

Рейтинг

Источник

Математика 2 класс учебник Петерсон 1 часть — страница 63

Подготовили готовое домашнее задание к упражнениям на 63 странице по предмету математика за 2 класс. Ответы на задания: 6, 7, 8, 9 и 10.

Учебник 1 часть — Страница 63.

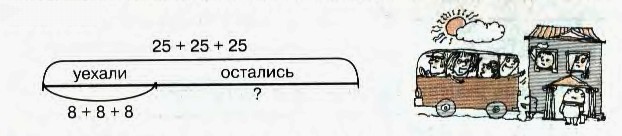
В трёх классах начальной школы по 25 человек. По 8 учеников из каждого класса поехало на экскурсию. Сколько учеников осталось?

Чтобы ответить на вопрос задачи, то есть найти часть, нужно из общего количества детей (целого) вычесть части, которая уехала. Сразу мы это сделать не можем, так не знаем ни одного, ни другого. По условию задачи трёх классах начальной школы по 25 человек, поэтому общее число можно найти, сложив три раза по 25.
В задаче говорится, что на экскурсию поехало по 8 учеников из каждого класса, поэтому, если мы три раза сложим по 8, узнаем, сколько это человек всего.

1) 8 + 8 + 8 = 24 (чел.) – уехали.
2) 25 + 25 + 25 = 75 (чел.) – всего.
3) 75 – 24 = 51 (чел.)
Ответ: 51 человек остался.

Что общего у фигур слева и чем они отличаются от фигур справа?

Слева и справа одинаковые фигуры. Но слева маленькие фигурки находятся внутри больших, а справа они находятся снаружи, справа от больших.

Сложи из 17 палочек данную фигуру:
а) Убери 3 палочки так, чтобы получилось 4 равных квадрата.
б) Убери 2 палочки так, чтобы получилось 5 равных квадратов. Сколько различных решений ты сможешь найти?

Какое число может быть лишним: а) 20, 14, 17, 11; 6) 4, 1, 16, 8, 2; в) 305, 35, 215,125?
Расположи данные числа в порядке возрастания, найди закономерность и запиши следующие 3 числа.

Варианты выбора лишнего числа могут быть различными.

а) 20 – круглое число, а остальные – нет; 11 – записано одинаковыми цифрами, а остальные – нет.
В полученном ряду числа увеличиваются на 3: 11, 14, 17, 20, 23, 26, 29.

б) 16 – двузначное число, а остальные – однозначные; 1 – нельзя представить в виде суммы одинаковых слагаемых, а остальные – можно.
В полученном ряду числа удваиваются (складываются сами с собой): 1, 2, 4, 8, 16, 32, 64, 128.

в) 35 – двузначное число, а остальные – трехзначные; 305 – у данного числа в разряде десятков отсутствуют единицы, а у остальных – нет.
В полученном ряду числа увеличиваются на 90: 35, 125, 215, 305, 395, 485, 575.

Рейтинг

Источник

Пушкин сделал!

Разбор домашних заданий 1-4 класс

Home » Петерсон Математика » Л.Г. Петерсон Математика 2 класс Ответы Урок 32 Вычитание трехзначных чисел: 231-145

Л.Г. Петерсон Математика 2 класс Ответы Урок 32 Вычитание трехзначных чисел: 231-145

1. Пользуясь схемой, объясни смысл равенств, назови в них части и целое. Какими способами можно проверить правильность решения примеров на сложение и вычитание?

Чтобы проверить пример на сложение, нужно из целого вычесть какую−либо часть.
Чтобы проверить пример на вычитание, нужно сложить части и получить целое.

2. Используя рисунок, объясни решение примера. Что ты замечаешь? Сделай вывод.

В числе 231 из одного десятка взяли 10 единиц, а из 1 сотни взяли 10 десятков. Затем произвели поразрядно вычитание.

348 − x = 265
x = 348 − 265
x = 83
Проверка:
348-83=265

x + 738 = 856
x = 856 − 738
x = 118
Проверка:
118+738=856

x − 524 = 97
x = 97 + 524
x = 621
Проверка:
621-524=97

В трех вторых классах учится 90 человек. Во 2 «А» учится 34 человека, а во 2 «Б» − на 5 человек меньше, чем во 2 «А». Сколько человек учится во 2″В»? Какие еще вопросы можно поставить к этому условию?

1) 34 − 5 = 29 (человек) − учится во 2 «Б» классе;
2) 34 + 29 = 63 (человека) − учатся во 2 «А» и во 2 «Б» классе вместе;
3) 90 − 63 = 27 (человек) − учатся во 2 «В» классе.
Ответ: во 2 «В» классе учится 27 человек.

Сколько всего человек во 2 «Б» и 2 «В» классе?
29 + 27 = 56 (человек)
На сколько человек больше во 2 «А» классе, чем во 2 «В»?
34 − 27 = 7 (человек).

4 м 29 см + 2 м 96 см = 429 см + 296 см = 725 см = 7 м 2 дм 5 см

5 м 42 см − 4 м 86 см = 542 см − 486 см = 56 см = 5 дм 6 см

3 м 7 см + 15 дм 8 см = 307 см + 158 см = 465 см = 4 м 6 дм 5 см

86 дм 1 см − 2 м 9 дм = 861 см − 290 см = 571 см = 5 м 7 дм 1 см

7. В трех классах школы по 25 учеников. По 8 учеников из каждого класса поехало на экскурсию. Сколько учеников осталось?

1) 25 + 25 + 25 = 50 + 25 = 75 (учеников) − всего учится в трех классах;
2) 8 + 8 + 8 = 16 + 8 = 24 (ученика) − поехали на экскурсию;
3) 75 − 24 = 51 (ученик) − остался в школе.

Ответ: в школе остался 51 ученик

8. Сложи из 17 палочек данную фигуру.
а) Убери две палочки так, чтобы получилось 5 равных квадратов.
б) Убери три палочки так, чтобы получилось 4 равных квадрата.
Имеются ли другие решения?

Для задания а возможны 4 варианта решения, для б — 5 вариантов

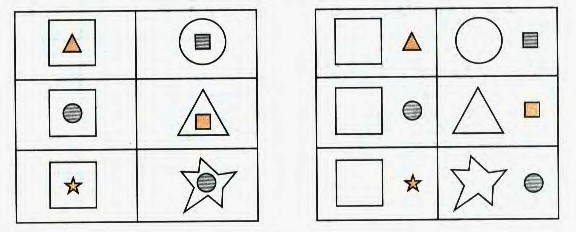
9. Что общего у фигур слева, чем они отличаются от фигур справа?

Общее у фигур слева:

Также дополнительно можно указать:

Фигуры справа отличаются от фигур слева тем, что у них маленькая фигура расположена рядом, а не внутри.

Какое число может быть лишним? Расположи числа в порядке возрастания, найди закономерность и запиши следующие три числа.

а) 20, 14, 17, 11;

б) 4, 1, 16, 8, 2;

в) 305, 35, 215, 125.

а) лишним может быть число 20, у него у единственного 0 в разряде единиц. Также лишним может быть число 11, у него единственного 2 одинаковые цифры.

В порядке возрастания: 11, 14, 17, 20

Закономерность: проверим на сколько следующее число больше предыдущего

Значит каждое следующее число больше предыдущего на 3

11, 14, 17, 20, 23, 26, 29

б) лишним может быть число 16, оно единственное двузначное. Также лишней может быть единица как единственное нечетное число.

В порядке возрастания: 1, 2, 4, 8, 16

Закономерность: проверим на сколько следующее число больше предыдущего

Видим, что каждое следующее число является суммой предыдущего числа с самим собой: 2=1+1; 4=2+2; 8=4+4; 16=8+8

1, 2, 4, 8, 16, 32, 64, 128

в) лишним может быть число 35, оно единственное двузначное. Также лишним может быть число 305 как единственное число с нулем.

В порядке возрастания: 35, 125, 215, 305

Закономерность: проверим на сколько следующее число больше предыдущего

Значит каждое следующее число больше предыдущего на 90.

35, 125, 215, 305, 395, 485, 575

11. Игра «Магические квадраты»
Заполни таблицы так, чтобы в каждой таблице все суммы чисел в строках, столбцах и диагоналях были равны.

1 квадрат:
14 + 8 + 2 = 24 − сумма, которая должна быть в каждой диагонали, строке и столбце:

2 квадрат:
12 + 16 + 20 = 48 − сумма, которая должна быть в каждой диагонали, строке и столбце:

3 квадрат:
3 + 13 + 11 = 27 − сумма, которая должна быть в каждой диагонали, строке и столбце:

Источник

Что общего у фигур слева и чем отличаются справа петерсон

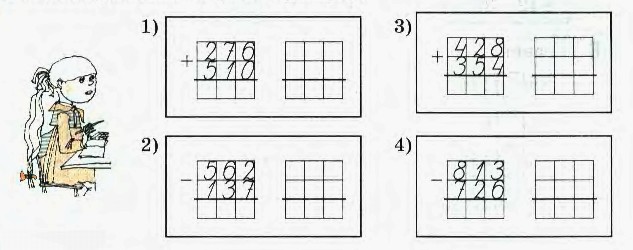
2. Выполни действия и сделай проверку:

4 м 29 см + 2 м 96 см 3 м 7 см + 15 дм 8 см

6. В трёх классах начальной школы по 25 человек. По 8 учеников из каждого класса поехало на экскурсию. Сколько учеников осталось?

7*. Что общего у фигур слева и чем они отличаются от фигур справа?

8. Сложи из 17 палочек данную фигуру:

а) Убери 3 палочки так, чтобы получилось 4 равных квадрата.
б) Убери 2 палочки так, чтобы получилось 5 равных квадратов. Сколько различных решений ты сможешь найти?

9*. Какое число может быть лишним:

а) 20, 14, 17, 11; б)4,1,16,8,2; в) 305,35, 215, 125?

Расположи данные числа в порядке возрастания, найди закономерность и запиши последующие 3 числа.

_{Математика скачать, задача школьнику 2 класса, материалы по математике для 2 класса онлайн}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Источник

Полный решебник (ответы на вопросы) (Л.Г. Петерсон, Н.П. Холина, «Раз-ступенька, два-ступенька…» Математика для детей 5-6 лет, часть 1) (стр 16-29)

Здесь представлены ответы на вопросы, подсказки (решебник) по пособию Л.Г. Петерсон и Н.П. Холиной («Раз-ступенька, два-ступенька…» Математика для детей 5-6 лет, часть 1) в помощь родителям учеников.

Некоторые задания с очевидными решениями здесь не разбираются.

3. Прочитайте ребенку задание 2 или 3 раза. Если он скажет, что понял, как выполнять – пусть выполнит. Проконтролируйте точность выполнения задания.

Над чертой должно быть два синих круга, а под чертой – три желтых треугольника.

Два раза прочитайте ребенку задание, проверьте: справа от линии должно быть 3 желтых круга, слева – 2 зеленых квадрата.

4. Внимание! В подобных примерах ошибки подразумеваются только в сумме. В слагаемых ошибок нет. Для сравнения можно подчеркивать элементы слева и справа от знака равно.

а) дорисовать зеленый треугольник в сумме;

б) поменять слагаемые местами.

а) в сумме необходимо раскрасить квадрат в синий цвет;

б) поменять слагаемые местами.

а) вычеркнуть синий круг в сумме;

б) поменять слагаемые местами.

1. В правом задании есть некоторая неоднозначность (методическая недоработка): по правую лапу от крокодила Гены стоит Чебурашка, а в правой части рисунка – щенок. Можно просто пропустить задание 1б.

2. Аналогичное соображение для рисунка справа.

3. Должно быть 3 желтых квадрата справа от красной линии, слева от зеленой линии – 3 синих овала.

4. Лишний элемент – ветка сосны.

а) первое слагаемое – синий цветок;

б) второе слагаемое – желтый треугольник и красный круг.

а) сумма: зеленый квадрат, красный треугольник, желтый круг, синий треугольник;

б) первое слагаемое: синий треугольник.

Предлагаю выучить с ребенком правило: от перестановки слагаемых сумма не меняется.

7. Каждый раз убираем справа по одному квадрату и добавляем по одному кругу слева.

1. Знак «минус» обозначает действие вычитание.

С чем сравнивают вычитание для детей:

В большом мешке были какие-то предметы. То, что стоит слева от знака «минус» – было в мешке. То, что стоит справа от знака «минус» – вытаскивают из мешка. То, что стоит справа от знака «равно» – остается в мешке.

В примере 1а в мешке было: Два больших красных мячи и три маленьких синих мяча. Из мешка вытащили три маленьких синих мяча. В мешке осталось два больших красных мяча.

Вводим слова: уменьшаемое, вычитаемое, разность.

То, что слева от знака минус называется уменьшаемым.

То, что справа от знака минус называется вычитаемым.

То, что стоит справа от знака равно называется разностью.

В примере 1б разность равна трем маленьким синим мячам.

а) разность – красный круг;

б) разность – два желтых треугольника;

в) разность – два красных круга;

г) разность – два синих квадрата.

3. Все варианты подсказать невозможно. Проконтролируйте правильность выполнения задания. Меняется только один признак (форма, размер или цвет).

1. Цветок нарисовать у почтальона, красным обвести кота Матроскина.

а) разность – красный флаг;

б) разность – синий цветок и желтый шар;

в) разность – синий треугольник, красный треугольник;

г) разность – желтый квадрат, зеленый круг.

1) первое решение – большой треугольник, выделяем по размеру

2) второе решение – круг, выделяем по форме

3) третье решение – красный треугольник, выделяем по цвету

Вводим понятие «части» и «целого». Для сложения: два слагаемых – это «части», «целое» – это сумма. Для вычитания: уменьшаемое – это «целое», вычитаемое и разность – это «части».

а) сумма – два синих квадрата, два красных круга, желтый круг;

б) поменять местами слагаемые, сумма – та же;

а) разность – красный треугольник, желтый круг;

б) сумма – синий квадрат, два красных круга, желтый треугольник.

Фигуры сгруппированы по цвету, можно сгруппировать по форме:

Источник