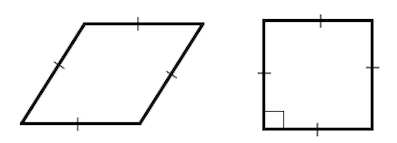Что общего у квадрата и ромба

Разница между ромбом и квадратом

Взрослому человеку такой вопрос может показаться наивным, а вот школьники и маленькие дети часто задают его. И порой одной лишь демонстрации геометрических фигур может оказаться мало. Поэтому несколько простых закономерностей помогут разобраться и понять отличия между указанными категориями.

Определение

Ромб – это четырёхугольная геометрическая фигура, все стороны которой равны. Противоположные стороны параллелограмма параллельны, а диагонали всегда пересекаются под углом в 90 градусов и делят угол пополам.

Ромб

Квадрат – это ромб, внутренние углы которого составляют 90 градусов, а все стороны равны. Его главная особенность – полная симметричность, что послужило широкому распространению геометрической фигуры. Диагонали делят квадрат на 4 одинаковых прямоугольных треугольника.

Сравнение

Итак, вопрос действительно несложен. Ромб – понятие более широкое, и квадрат – всего лишь специфический вид данной фигуры. Многие их свойства абсолютно идентичны. У квадрата и ромба все стороны равны, а диагонали пересекаются под прямым углом. Тем не менее, есть некоторые фундаментальные различия. У квадрата все внутренние углы равны и составляют 90 градусов, у ромба равны лишь противоположные углы. Подсчитать площадь квадрата легко: нужно умножить длину стороны на себя же. Чтобы узнать площадь ромба, нужно перемножить его диагонали, а полученный результат разделить на два.

Источник

Основные геометрические фигуры

Основные понятия

Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.

Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.

Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.

Обучение на курсах по математике поможет быстрее разобраться в видах и свойствах геометрических фигур.

Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.

Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.

Периметром принято называть сумму длин всех сторон многоугольника. Периметр обозначается заглавной латинской P.

Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Если все точки фигуры принадлежат одной плоскости, значит она является плоской.

Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.

Примеры объемных геометрических фигур:

Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.

Прямоугольник

Прямоугольник — параллелограмм, у которого все углы прямые.

Узнать площадь прямоугольника помогут следующие формулы:

Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.

Периметр прямоугольника — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Квадрат

Квадрат — это тот же прямоугольник, у которого все стороны равны.

Найти площадь квадрата легко:

Периметр квадрата — это длина стороны, умноженная на четыре.

P = 4 × a, где a — длина стороны.

Трапеция

Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.

Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.

Как найти площадь трапеции:

S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.

Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.

Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.

P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.

Параллелограмм и ромб

Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны

Ромб — это параллелограмм с равными сторонами.

Общие формулы расчета площади фигур:

Периметр ромба — это произведение длины стороны на четыре.

P = 4 × a, где a — длина стороны.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.

P = 2 × (a + b), где a — ширина, b — высота.

Треугольник

Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.

Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.

S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.

Основание может быть расположено иначе, например так:

При тупом угле высоту можно отразить на продолжение основания:

При прямом угле основанием и высотой будут его катеты:

S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.

Периметр треугольника — это сумма длин трех его сторон.

P = a + b + c, где a, b, c — длина стороны.

Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.

P = 3 × a, где a — длина стороны.

Круг — это это часть плоскости, которая лежит внутри окружности.

Окружность — это граница круга.

Радиус окружности — это расстояние от центра окружности до любой точки на ней.

Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.

Формулы площади круга:

Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.

L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.

Источник

Определи общие свойства квадрата и ромба?

Определи общие свойства квадрата и ромба.

Чем отличаются эти фигуры?

Квадрат – это одна из разновидностей ромба.

Обе фигуры имеют по

четыре стороны и четыре угла.

При этом у каждой из фигур, и у квадрата, и

у ромба, все стороны обязательно должны быть одинаковой длины.

Главное отличие ромба от квадрата в величине углов.

между собой только противолежащие углы.

У квадрата же все четыре угла

имеют одинаковую величину.

Общие свойства квадрата и ромба : У них 4 угла, и у квадрата, и у ромба.

Ромб– это четырёхугольная геометрическая фигура, все стороны которой равны.

Противоположные стороны параллелограмма параллельны, а диагонали всегда пересекаются под углом в 90 градусов и делят угол пополам.

Отличие ромба от квадрата :

Квадрат – частный случай ромба.

Второе понятие является более широким.

У квадрата все углы равны 90 градусов, у ромба данное значение может варьироваться.

Узнать площадь ромба проще всего, перемножив диагонали и разделив на 2.

У квадрата действие ещё проще : достаточно одну сторону умножить на саму себя.

Какая фигура является пересечением общей частью : квадрата и луча двух квадратов?

Какая фигура является пересечением общей частью : квадрата и луча двух квадратов.

Начерти фигуры четырехугольник (не прямоугольник и не квадрат)?

Начерти фигуры четырехугольник (не прямоугольник и не квадрат).

Прямоугольник (не квадрат).

Что общего у всех этих фигур?

Какой класс, из указанных в ответах.

Не может быть в этом разбиении?

1. Множество геометрических фигур.

2. Множество ромбов, не являющихся квадратами.

3. Множество квадратов.

4. Множество треугольников.

Дорисуй в каждой фигуре по одному квадрату так, чтобы все фигуры отличались друг от друга только цветом?

Дорисуй в каждой фигуре по одному квадрату так, чтобы все фигуры отличались друг от друга только цветом.

Чем отличается квадрат от ромба или ромб от квадрата?

Чем отличается квадрат от ромба или ромб от квадрата.

Напишите 6 примеров.

Дам за это 25 баллов.

Сравни все фигуры между собой : чем они похожи, чем различаются?

Дорисуй в каждой фигуре по одному квадрату так, чтобы все фигуры отличались друг от друга только цветом.

Какая фигура является пересечением (общей частью) : 1)Квадрата и луча ; 2)двух квадратов?

Какая фигура является пересечением (общей частью) : 1)Квадрата и луча ; 2)двух квадратов?

Запиши одно общее свойство фигур?

Запиши одно общее свойство фигур.

Какие общие свойства имеют ромб, квадрат и прямоугольник?

Какие общие свойства имеют ромб, квадрат и прямоугольник.

Как может называться множество <квадрат, ромб, круг >?

Как может называться множество <квадрат, ромб, круг >.

Дополните это множество названием еще двух фигур.

83 : 9 = 9(2ост. ) 61 : 8 = 7(5ост) 94 : 15 = 6(4ост) 678 : 74 = 9(12ост) 185 : 19 = 9(14ост) 312 : 48 = 6(24ост) 1384 : 275 = 5(9ост) 2062 : 412 = 5(2ост. ) 3581 : 403 = 8(277ост. ) вроде так).

132 = 2 * 2 * 3 * 11 297 = 3 * 3 * 3 * 11 НОД(132, 297) = 3 * 11 = 33 99 = 3 * 3 * 11 252 = 2 * 2 * 3 * 3 * 7 НОД(99, 252) = 3 * 3 = 9 120 = 2 * 2 * 2 * 3 * 5 165 = 3 * 5 * 11 НОД(120, 165) = 3 * 5 = 15 120 = 2 * 2 * 2 * 3 * 5 363 = 3 * 11 * 11 НОД(1..

Длинну второй стороны возьмем за х тогда длина третьей стороны х + 10 Длина первой стороны х + 10 + 12 = х + 22 Длина четвертой х + 10 + 12 + 10 = х + 32 периметр = х + х + 10 + х + 22 + х + 32 = 104 4х + 64 = 104 4х = 40 х = 10 = длина второй сторон..

Источник

Чем отличается ромб от квадрата

Взрослому человеку такой вопрос может показаться наивным, а вот школьники и маленькие дети часто задают его. И порой одной лишь демонстрации геометрических фигур может оказаться мало. Поэтому несколько простых закономерностей помогут разобраться и понять отличия между указанными категориями.

Что такое ромб и квадрат

Ромб – это четырёхугольная геометрическая фигура, все стороны которой равны. Противоположные стороны параллелограмма параллельны, а диагонали всегда пересекаются под углом в 90 градусов и делят угол пополам.
Ромб
Квадрат – это ромб, внутренние углы которого составляют 90 градусов, а все стороны равны. Его главная особенность – полная симметричность, что послужило широкому распространению геометрической фигуры. Диагонали делят квадрат на 4 одинаковых прямоугольных треугольника.

Разница между ромбом и квадратом

Итак, вопрос действительно несложен. Ромб – понятие более широкое, и квадрат – всего лишь специфический вид данной фигуры. Многие их свойства абсолютно идентичны. У квадрата и ромба все стороны равны, а диагонали пересекаются под прямым углом. Тем не менее, есть некоторые фундаментальные различия. У квадрата все внутренние углы равны и составляют 90 градусов, у ромба равны лишь противоположные углы. Подсчитать площадь квадрата легко: нужно умножить длину стороны на себя же. Чтобы узнать площадь ромба, нужно перемножить его диагонали, а полученный результат разделить на два.

TheDifference.ru определил, что отличие ромба от квадрата заключается в следующем:

Объём понятия. Квадрат – частный случай ромба. Второе понятие является более широким.
Внутренние углы. У квадрата все углы равны 90 градусов, у ромба данное значение может варьироваться.
Вычисление площади. Узнать площадь ромба проще всего, перемножив диагонали и разделив на 2. У квадрата действие ещё проще: достаточно одну сторону умножить на саму себя.

Источник

Ромб. Свойства и признаки ромба

Ромб – это параллелограмм, у которого все стороны равны.

Если у ромба – прямые углы, то он называется квадратом.

Свойства ромба

1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.

Помимо этого:

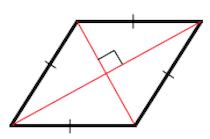
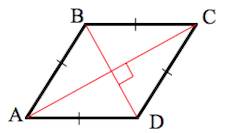
2. Диагонали ромба перпендикулярны.

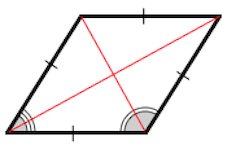
3. Диагонали ромба являются биссектрисами его углов.

4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

Признаки ромба

Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:

1. Все стороны параллелограмма равны между собой ().

2. Диагонали пересекаются под прямым углом ().

3. Диагонали параллелограмма являются биссектрисами его углов.

Площадь ромба

Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник