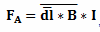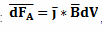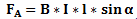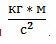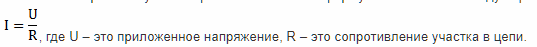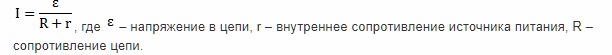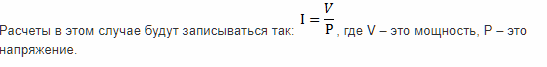Что означает крестик и точка в физике
В чем измеряется сила тока: правило буравчика и правой руки
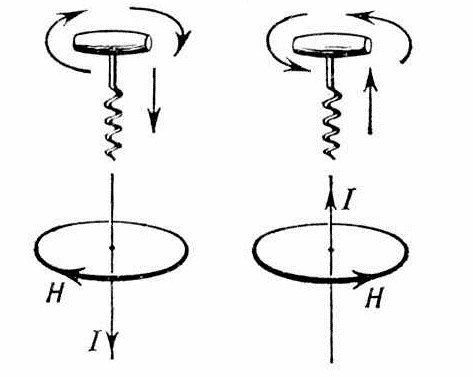
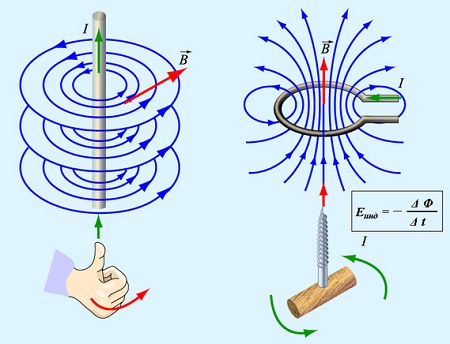
Для того, чтобы узнать траекторию вращения магнитного поля, находящегося у прямого проводника с током, используется правило буравчика (штопора). В литературе также оно известно, как правило правой руки. В научной среде выделяют и правило левой руки. …
Применение правила буравчика
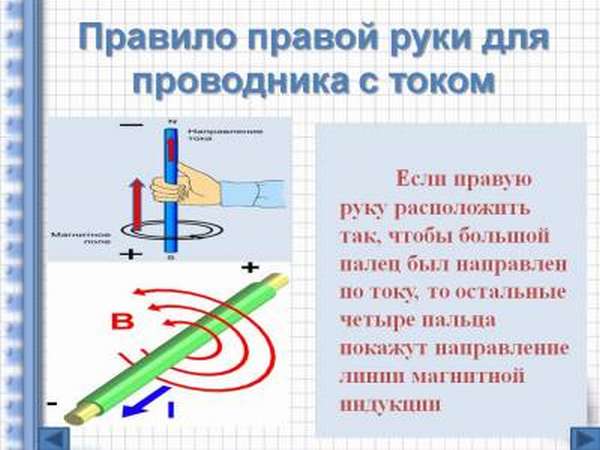
Чтобы определить траекторию вращения магнитного контура на представленном графическом изображении нужно знать несколько особенностей.
Часто в задачах по физике нужно, наоборот, определить траекторию движения тока. Чтобы это сделать, дается направление вращения кругов магнитного поля. Ручка буравчика начинается вращаться в сторону, указанную в условиях. Если буравчик движется в поступательном направлении, значит, ток направлен в сторону движения, если же он направлен в обратную, то и ток движется соответственно.
Для определения траектории движения тока в случае, представленном на втором рисунке, тоже можно воспользоваться правилом штопора. Для этого необходимо вращать ручку буравчика в сторону, указанную на изображении контура магнитного поля. Если он будет двигаться поступательно, то ток будет двигаться в сторону от наблюдателя, если же, наоборот, только к наблюдателю.
Важно! Если указана траектория движения потока, то определить траекторию вращения линии магнитного контура можно по вращению ручки буравчика.
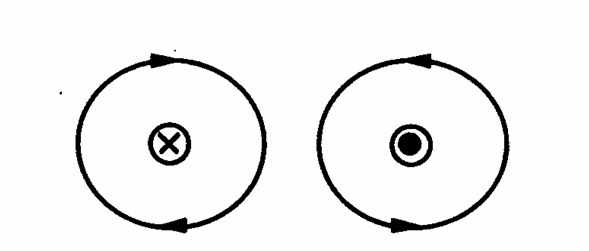
Оно обозначается при помощи точки или крестика. Точка означает движение в сторону наблюдателя, крестик означает обратное. Легко запомнить этот случай, используя так называемое правило «стрелы», если острие «смотрит», а в лицо, то траектория движения тока в сторону наблюдателя, если же в лицо «смотрит хвост стрелы», то она двигается от наблюдателя.
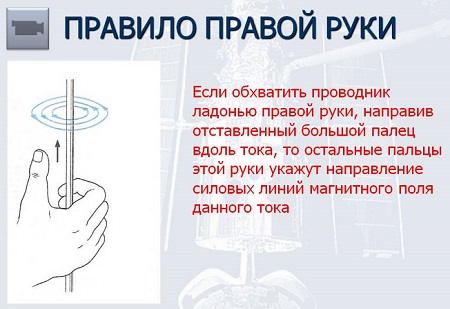
Как правило буравчика, так и правило правой руки, достаточно легко применить на практике. Для этого нужно расположить кисть соответствующей руки таким образом, чтобы в лицевую сторону направлялся силовой контур магнитного поля, после чего большой палец, отведенный перпендикулярно, необходимо направить сторону движения тока, соответственно, остальные выпрямленные пальцы укажут на траекторию магнитного контура.
Различают исключительные случаи использования правила правой руки для вычисления:
Правило левой руки
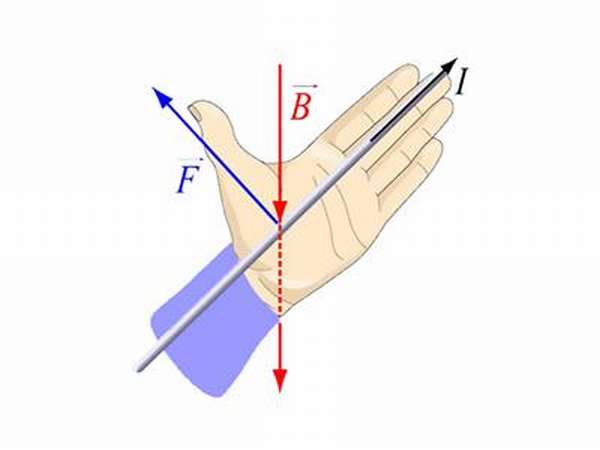
Возможно определить и направление тока, если доступна информация о траекториях вращения магнитного контура и действующей на проводник энергии. Определяется и направление магнитного контура в случае известности траектории движения силы и тока. Ну и можно выяснить знак заряда нестатичной частицы.
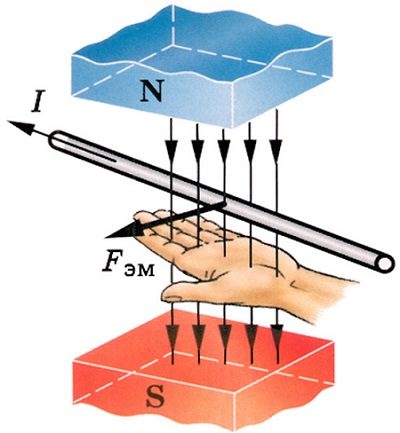
Это правило звучит следующим образом: расположив лицевую часть кисти соответствующей руки, чтобы воображаемый контур магнитного поля направлялись в нее под прямым углом, а пальцы, за исключением большого, направив в сторону движения тока, можно определить траекторию силы, воздействующая на этот провод при помощи перпендикулярно отодвинутого большого пальца. Сила, оказывающая воздействие на проводник, носит имя Мари Ампера, обнаружившего ее в 1820 году.
Сила Ампера: варианты расчета
Прежде чем сформулировать данную величину, необходимо разобраться, что такое понятие сила в физике. Ей называется величина в физике, которая является мерой воздействия всех окружающих тел на рассматриваемый объект. Обычно любую силу обозначают английской буквой F, от латинского fortis, что означает сильный.
Рассчитывается элементарная сила Ампера по формуле:
где, dl – часть длины проводника, B –индукция магнитного контура, I – сила тока.
Рассчитывается также сила Ампера по формуле:
где, J – направление плотности тока, dv– элемент объема проводника.
Формулировка расчета модуля силы Ампера, согласно литературе, звучит так: данный показатель напрямую зависит от силы тока, протяженности проводника, синуса, образуемого между этим вектором и самим проводником угла, и величины значения вектора магнитного контура в модуле. Она и носит название модуля силы Ампера. Формула данного закона математически строится так:
где, B – модуль индукции магнитного контура, I – сила тока, l – длина проводника, α – образуемый угол. Максимальное значение будет при перпендикулярном их пересечении.
Показатель измеряется в ньютонах (условное обозначение – Н) или
. Он является векторной величиной и зависит от вектора индукции и тока.
Существуют и другие формулы для расчета силы Ампера. Но на практике они достаточно редко востребованы и тяжелы для понимания.
Сила тока
Иногда чтобы рассчитать закон Ампера, для начала нужно вычислить силу тока. Существуют несколько формул расчета данной величины. Для расчета ее величины используют:
Самым популярным является отношение количество заряда прошедшего за единицу времени через определенную поверхность к размеру этого интервала. Графически формула выглядит следующим образом:
Чтобы найти этот показатель можно пользоваться законом Ома для участка цепи. Он гласит следующее: величина этого показателя равна отношению приложенного напряжения к сопротивлению на измеряемым участке цепи. Записывается формула этого закона следующим образом:
Определить ее также можно, применив формулу закон Ома для полной цепи. Звучит он так: эта величина является отношением приложенного напряжения в цепи и суммы внутреннего сопротивления источника питания и всего сопротивления в цепи. Формула выглядит так:
Рассчитать данную величину можно, в случае если известны мощность и напряжение.
Важно! Применение каждой конкретной формулы зависит от имеющихся в распоряжении данных.
Согласно утвержденной МСЕ, измеряется сила тока в амперах, и обозначается А (в честь ученого, открывшего ее). Но это не единственный способ обозначения данной величины. Дополнительно измеряется сила тока в Кл/с.
Изучая в общеобразовательных учреждениях данный материал, ученики быстро забывают, как применять правила левой и правой руки, и для чего они вообще нужны. Также часто они не помнят в чём измеряют указанные величины. Ознакомившись с рассмотренным выше материалом, не должно возникнуть трудностей с применением рассмотренных правил и законов на практике.
Правило левой руки точка и крестик
В физике и электротехнике широко используются различные приемы и способы, позволяющие определить одну из характеристик магнитного поля – направленность напряженности. С этой целью используется закон буравчика, правой и левой руки. Данные способы позволяют получить довольно точные результаты.
Правило буравчика и правой руки
Закон буравчика используется для определения направленности напряженности магнитного поля. Оно работает при условии прямолинейного расположения магнитного поля, относительно проводника с током.
Это правило заключается в совпадении направленности магнитного поля с направленностью рукоятки буравчика, при условии вкручивания буравчика с правой нарезкой в направлении электрического тока. Данное правило применяется и для соленоидов. В этом случае, большой палец, оттопыренный на правой руке, указывает направление линий магнитной индукции. При этом, соленоид обхватывается так, что пальцы указывают направление тока в его витках. Обязательным условием является превышение длиной катушки ее диаметра.
Правило правой руки противоположно правилу буравчика. При обхватывании исследуемого элемента, пальцы в сжатом кулаке указывают направление магнитных линий. При этом, учитывается поступательное движение по направлению магнитных линий. Большой палец, который отогнут на 90 градусов по отношению к ладони, указывает направление тока.
При движущемся проводнике, силовые линии перпендикулярно входят в ладонь. Большой палец руки вытянут перпендикулярно, и указывает направление движения проводника. Оставшиеся четыре оттопыренных пальца, расположены в направлении индукционного тока.
Правило левой руки
Правило левой руки формулируется еще и таким образом, что четыре пальца на левой руке располагаются в направлении, куда движутся положительные или отрицательные частицы электрического тока. Индукционные линии, как и в других случаях, должны перпендикулярно располагаться относительно ладони и входить в нее. Большой оттопыренный палец указывает на направление силы Ампера или Лоренца.

Общие правила
Существует несколько для вариантов, чтобы указать направление перпендикулярного отрезка к двум исходным векторам и определить ориентацию базиса. В физике есть такие важные направления:
Выбор пути аксиальной величины является условным, но он происходит одинаково, поэтому в конечном значении знак остается постоянным. Правила и способы помогают сохранять единый выбор:
С помощью этих правил выбирается направление векторного произведения и базисов (или одного из двух взаимосвязанных понятий). Прием используется для определения направлений основных величин взамен применения остальных методов, если иметь представление о порядке расположения множителей в соответствующих формулах.
Способы выбора правила сочетаются между собой для вычисления положительного пути произведения векторов и базиса (координатной системы) в пространстве. Базис определяется как скоординированный векторный набор, при этом любой вектор в пространстве представляется в едином варианте линейного соотношения векторов из этого пакета.
Использование правила буравчика из физики приводит к главным выводам:
Можно применять специальные правила для определения направляющих характеристик стержня, который движется в электромагнитном поле. Этими формулировками пользуются в различных конкретных ситуациях, но они являются менее общими по значению.
Правая и левая системы координат
Чтобы выяснить направление прямоугольных векторных координат, которые используются для показания отрезков любого курса, исходят из правила для чайников, что абсцисса и ордината направленного луча находятся в исходной точке пространства и совпадают с характеристиками их окончания.
Для случаев, когда координаты не совпадают, нужно сделать:
На плоскости прямоугольных координат расположение отрезка совпадает с ортогональной проекцией луча на координатную направляющую ось. Правило буравчика позволяет применять правый базис, но отход от негласного закона оговаривается отдельно. Эти правила условны, но сочетание векторов устанавливается так, что для базиса декартовой прямоугольной плоскости с одинаковым масштабированием по любым осям выполняются следующие законы:
Правила согласовываются между собой для определения курса векторного произведения и законов построения (выбора) положительного набора векторных отрезков.
Для векторного произведения
Правило буравчика и правой руки для векторного результата гласит, что, если изобразить отрезки так, чтобы совпадали их истоки, и поворачивать первый вектор по наиболее краткому пути по отношению ко второму лучу, то винт будет вращаться в направлении произведения векторов. В качестве винта подразумевается буравчик с правой нарезанной резьбой или с правым винтиком на конце, который встречается часто в списке рабочих инструментов. Этот закон можно переформулировать для стрелки часов, так как правое вращение винта идентично перемещению указателя на циферблате.

Если при таком положении наблюдателя и однотипном вращении с предыдущим случаем ставятся пальцы кисти справа, как бы сжимая поворачивающийся стержень, то они указывают направление витков. Палец, который располагается под углом 90°, определяет курс векторного произведения.
Если векторы изображаются так, что их истоки находятся в одной точке, палец правой кисти ставится по первому вектору-множителю, а указательный — параллельно второму вектору, то средний приблизительно укажет курс векторного произведения для закона буравчика. Физика в таком случае определяет направление:
Соотношение отрезков, абсцисс и ординат
Векторное соотношение двух отрезков, которые взаимодействуют в трехмерном пространстве, определяется лучом, расположенным перпендикулярно обоим начальным потокам. Длина произведения векторов равняется значению площади параллелограмма между начальными отрезками. Направление этих двух лучей выбирается так, чтобы три по порядку расположенных вектора из набора и результативных отрезков были правыми. Результат умножения векторов коллинеарного типа приравнивается к нулю, если один из них является отрезком с нулевым значением.

Формулы отличаются по знаку для нахождения координат произведения лучевых векторов через ординаты и абсциссы начальных отрезков в левой и правой системе прямоугольной структуры. Результат сочетания векторов является антикоммутационным, так как в отличие от скалярного результата в итоге имеет также вектор.
Модуль произведения векторов также является результатом перемножения модулей отрезков, если величины располагаются перпендикулярно друг к другу. Значение модуля стремится к нулю в случае коллинеарности лучей. Произведение векторов определяется в физических и технических дополнениях. Например, импульсный момент и действие Лоренца заносятся в данные по форме результата перемножения элементов из векторного набора.
Для упорядоченного набора лучей
Все разнообразные применяемые правила винта или законы обеих рук в электротехнике и физике не являются обязательными к использованию, если направление характеристик электромагнитного поля можно определить основными правилами одновременно со знанием формул для подсчета векторного соотношения. Малораспространенные правила характерны для особых случаев, когда их использование является удобным для быстрого выявления элементарных показателей системы.
Правила для базиса переписаны в виде:
Такие манипуляции расширяют возможности определения курса в координатном пространстве. Закон буравчика для базиса может заменить общее правило винта, правой кисти и других. Для его применения у наблюдателя должно быть развито некоторое пространственное воображение, так как требуется мысленно осуществлять поворот нарисованных векторов до того момента, пока они не совпадут с базисом. Набор векторов может при этом располагаться случайно.
Принцип для механического вращения
Отрезок вращения взаимно связывается с вектором угловой скорости поворота и лучом, начинающимся в неподвижной точке, приведенным в искомое положение. Величина определяется как произведение векторов. Угловая скорость представляет собой быстроту оборотов материального элемента вокруг центра.
Угловая скорость выражается:
Для определения курса модуля отрезка применяются правило винта и правой кисти, эффективно используемые в случае нахождения векторного произведения. Иногда этого хватает, но при реальном вращении законы формулируются в запоминающемся и простом варианте для нахождения направлений:
Для определения направления момента импульса, который меняется прямо пропорционально угловому вращению (скорости) с коэффициентом положительного импульса, применяются правила для нахождения показателей механического кручения.
Определение силового момента
Крутящий и вращательный момент представляет собой физический формат, равный произведению векторов силы и радиуса, проведенных от центральной оси к точке действия силы. Характеристики показывают силовое действие на твердом предмете.
Правила аналогичны предыдущим случаям, но отличаются незначительными деталями:
Электродинамика и магнитостатика
Магнитная индукция представляет собой векторный фактор, который характеризует силовое поле. Величина показывает влияние магнитного фона на отрицательно и положительно заряженные частицы в исследуемом пространстве. Индукция определяет силу влияния поля на заряд, перемещающийся с заданной скоростью. Для этого случая законы применения описываются так:
Для подвижного проводника
В стержне из металла находится большое число свободных электронов, движение которых характеризуется как хаотичное. Если катушка движется в силовом электромагнитном поле вдоль линий, то фон отклоняет электроны, перемещающиеся одновременно с проводником. Их движение создает ЭДС (электродвижущую силу) и называется электромагнитной наведенной индукцией.
Под действием индукции заряженные частицы передвигаются и накапливаются в одном конце стержня, при этом на другом проявляется нехватка электронов. В результате такой ситуации зарождается положительный заряд и возникает разность потенциалов, появляется напряжение электричества.
Ток будет протекать под действием разности потенциалов при подсоединении такой катушки к внешней цепи по замкнутому контуру. При передвижении стержня по направлению силовых линий снижается до нуля воздействие поля на заряды. Не возникает электродвижущая сила, нет напряжения, отсутствует ток электронов.
ЭДС индукции равняется произведению рабочего размера проводника, скорости движения стержня и значения магнитной индукции. Ее направление устанавливается по закону правой руки. Ладонь располагается так, чтобы в нее были направлены линии силового поля, а отогнутый под 90° большой палец ставится вдоль движения стержня. В этом положении четыре распрямленных пальца покажут курс тока индукции.
Нахождение ЭДС по Максвеллу
Электродвижущее давление будет возникать при каждом пересечении стержня и силового поля. Результативным будет перемещение проводника, самого поля или изменение электромагнитных характеристик силового пространства.
ЭДС, полученная в контуре при состыковке его с изменяющимся силовым полем, измеряется скоростью трансформации магнитного потока. Направление индуцированной движущей силы идет так, что продуцируемый ею электрический ток противодействует реконструкции потоков магнитного излучения.

Если вращать буравчик по путям завихрения пространства, где возникают векторы, то его движение покажет направление кручения ротора. Это можно проследить, если четыре сжатых пальца правой кисти поставить по курсу завихрения. В этом случае отогнутый палец укажет путь движения ротора.
При растущем значении магнитного потока большой палец под прямым углом покажет прямое движение силового потока через контурные линии. В случае убывания электромагнитного излучения палец будет свидетельствовать об обратном направлении. Согнутые четыре пальца будут располагаться по путям противоположного направления ЭДС в контуре.
Для магнитного вектора индукции правила буравчика совпадают с законом Ампера — Максвелла. Но к электротоку через контур добавляется скорость трансформации силового поля через эту конфигурацию, а магнитное поле воспринимается только в случае его перемещения в пределах очертания.
Применение правил левой кисти:
Принцип винта или закон Максвелла для правой руки используется для прямого стержня с током. Но в электротехнике есть много случаев применения катушек, в которых проводник не является прямолинейной формой. Например, соленоид, в котором присутствует витковая обмотка провода.
Правило правой кисти для соленоида: нужно взять катушку индуктивности в правую руку так, чтобы пальцы показывали путь тока в оборотах, отставленный под 90° большой палец определит курс магнитных линий во внутренней части устройства. Зная полярность, легко вычислить путь прохождения электрического тока.
Что ты хочешь узнать?
Ответ
Возьми отточенный карандаш. Представь, что по карандашу может протекать ток и течёт он от тупого конца к острию. Обхвати его ПРАВОЙ рукой так, чтобы отогнутый большой палец показывал К ОСТРИЮ. В какую сторону остальные пальцы повернулись для обхвата? Это и есть НАПРАВЛЕНИЕ МАГНИТНОЙ силовой линии данного тока.
Итак, ПРАВАЯ рука – хваталка.
А теперь распрями ЛЕВУЮ РУКУ, соединив четыре пальца, а большой отогнув перпендикулярно другим четырём пальцам. Теперь наш карандаш будет играть роль вектора ВНЕШНЕГО магнитного поля. Пусть этот вектор входит в раскрытую тобой ладонь ЛЕВОЙ руки, перпендикулярно ей. (Остриём карандаша тыкаешь себе в ладонь) При этом ладонь (её плоскость) будет иметь в пространстве вполне определённую ориентацию. Представь себе, что ты проткнула ладонь и она (ладонь) может вертеться на карандаше как кусок шашлыка на шампуре. ПОВЕРНИ ладонь так, чтобы ЧЕТЫРЕ сложенных пальца показали НАПРАВЛЕНИЕ тока. Отогнутый палец покажет направление СИЛЫ АМПЕРА или СИЛЫ ЛОРЕНЦА (Направление тока – движение ПОЛОЖИТЕЛЬНЫХ зарядов, цело кучи зарядов – это Ампер, а одиночный заряд – Лоренц)
ЛЕВАЯ рука – парализована. ЕЁ НЕЛЬЗЯ гнуть.
Подводим итог. Правая хваталка определяет магнитное поле тока, Левая парализовка – направление силы со стороны внешнего маг. поля на ток или ДВИЖУЩИЙСЯ заряд.
Принцип суперпозиции – Общее поле – ВЕКТОРНАЯ сумма всех полей. Складывать можно только ОДНОРОДНЫЕ величины. НЕЛЬЗЯ прибавить электрическое поле к магнитному, гравитационное к электрическому.
Надеюсь что внятно объяснил, а то, что немного с «кровавым» уклоном, так когда ткнёшь себя в ладонь острием, тут же вспомнишь правило)))