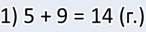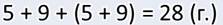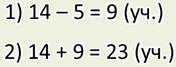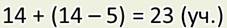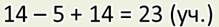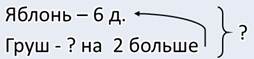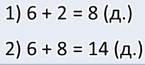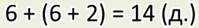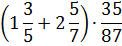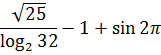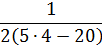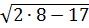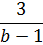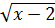Что означает реши задачу выражением

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 22. Решение текстовых задач. Запись решения выражением

Перечень вопросов, рассматриваемых в теме:

— Что такое встречное движение, расстояние?

— Как выполнять схематический чертёж к задачам на движение?

Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.

Выражение – формула, выражающая какие–либо математические отношения.

Расстояние – пространственный промежуток, разделяющий два объекта, отрезок пути.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

Теоретический материал для самостоятельного изучения

Расстояние – это путь, который прошёл какой-либо объект.

РАССТОЯНИЕ – промежуток в пространстве, разделяющий два объекта

Измеряя расстояние, мы будем использовать сокращённые записи.

Сегодня на уроке мы будем решать новые задачи – задачи на движение.

Длина аллеи 80 м. Два мальчика пошли навстречу друг другу. Один прошёл до встречи 45 м. Сколько прошёл до встречи другой мальчик?

Сделаем к задаче схематический чертёж.

Начертим отрезок, обозначающий длину всей дорожки, или расстояние между концами дорожки. Синей стрелкой обозначим длину дорожки. Укажем – 80 метров.

Мальчики шли навстречу друг другу с разных сторон дорожки. На чертеже это будем обозначать стрелками, которые показывают направление движения каждого мальчика.

Место встречи мальчиков будем обозначать флажком.

Теперь обозначим, что один мальчик прошёл до встречи 45 метров, а другой –

неизвестно. Поставим знак вопроса.

Так выглядит схематический чертёж к задаче. По чертежу видно, что нам необходимо найти разность отрезков, выполнить вычитание.

Чтобы узнать, сколько метров до встречи прошёл второй мальчик, вычтем из длины всей дорожки длину пути, который прошёл первый мальчик.

80 – 45 = 35 (м) прошёл второй мальчик.

Второй мальчик прошёл до встречи 35 метров.

Решим вторую задачу:

Девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна девочка прошла до встречи 30 м, другая на 4 метра меньше. Какой длины была дорожка?

Сделаем схематический чертёж к задаче.

Итак, нам надо найти длину всей дорожки. Для этого мы должны знать, сколько метров прошла каждая девочка. Мы знаем, сколько прошла первая девочка – 30 метров. А сколько прошла вторая девочка, нам надо узнать.

Будем решать задачу в два действия. Запишем первое действие:

1) 30 – 4 = 26 (м) прошла вторая девочка.

Вторая девочка прошла до встречи двадцать шесть метров.

Теперь можем ответить на вопрос задачи. Запишем второе действие:

2) 30 + 26 = 56 (м) длина дорожки.

Длина всей дорожки была 56 метров.

Вывод: Для решения задач на движение обычно выполняют чертёж, в котором стрелками показывают направление движения объектов. Движение может быть встречным или в противоположных направлениях.

1.Подберите схематический чертёж к задаче

Красная Шапочка отправилась в гости к бабушке. До дома бабушки нужно пройти 100 метров. Красная Шапочка уже прошла 70 метров. Сколько ей осталось пройти?

2.Соедините каждый чертёж с карточкой, на которой записано соответствующее решение задачи.

30 – 20

30 + 20

70 – 45

70 – 45

30 + 20

30 – 20

Источник

Запись решения задачи выражением

Урок 15. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Запись решения задачи выражением»

— Плюс. Плююююс! Ты где?

Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.

— Здравствуй, Минус. Как это я забыл! Включаю.

— Здравствуйте, Дорогие Плюс и Минус!

— Да, царица, мы Вас внимательно слушаем.

— Мы очень внимательно слушаем.

— Ну что же, приступим. Итак, вот первая задача:

Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.

— Всё, я готов! Могу даже объяснить, как я решал эту задачу.

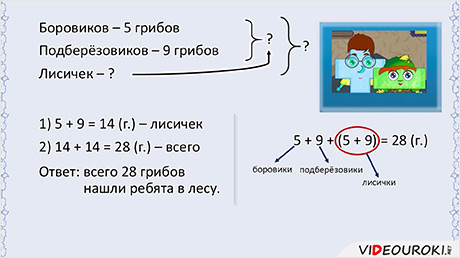
В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.

А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:

Ответ: всего 28 грибов нашли ребята в лесу.

— А я решал задачу другим способом. Вот посмотрите:

— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

Ответ: всего 23 учащихся присутствовало на уроке физкультуры.

— А вот я записал решение этой задачи по-другому:

И ещё можно вот так:

Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.

— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.

Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

— Ну что же, слушайте:

В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?

— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.

Значит, в саду царицы растёт 14 яблонь и груш.

А вот как получилась запись выражением:

— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

— Можно я начну первый.

Записывать решение задачи можно по действиям и выражением.

— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.

— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.

— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.

Источник

Различные способы решения задач и различные формы записи решения

Страницы работы

Содержание работы

На одном из уроков математики во II клас­се ученик, получив задание “Реши задачу”, спросил: “Каким способом нужно решать: по действиям или выражением”. Учитель ответил: “По действиям”.

Этот диалог показал, что и учитель, и уче­ник принимают различные формы запи­си решения за различные способы ее решения. Посещение уроков, беседы с учителями и учащимися позволили нам сде­лать вывод, что эта ошибка довольно распро­странена. Смешение же названных понятий приводит к тому, что, когда требуется дей­ствительно решить задачу разными способами, учащиеся либо вовсе не понимают задания, либо понимают его с большим трудом. А это, в свою очередь, снижает обучающие и воспитывающие возможности такого важного вида работы над задачей, как решение задач раз­ными способами.

Поэтому мы считаем своевременным обра­тить внимание учителей на отличие понятий способа решения задачи и формы записи решения задачи.

Задача считается решенной различными спо­собами, если се решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью использования этих связей.

Рассмотрим, например, задачу № 522 из учебника математики для II класса: “Для уро­ков труда купили 4 катушки белых ниток, по 10 коп. за катушку, и 6 катушек черных ни­ток по такой же цене. Сколько денег уплатили за эти нитки?”

Эта задача может быть решена двумя ариф­метическими способами.

При первом из них, наиболее очевидном, первоначально определяют стоимость черных ниток: (10-4)-коп., затем стоимость белых ни­ток: (10-6) коп. и, наконец, стоимость всех ниток.

При втором способе замечаем, что цена 1 катушки белых ниток та же, что и черных, поэтому вначале можно узнать, сколько всего катушек ниток купили (6+4), а затем опре­делить стоимость всех этих ниток

Запись решения, для каждого способа может быть выполнена в нескольких формах. Пока­жем все эти формы для каждого способа ре­шения.

Запись решения по действиям с пла­ном.

1. Сколько стоят белые нитки? 10·4 = 40 (коп.)

2. Сколько стоят черные нитки? 10·6=60 (коп.)

3. Сколько денег уплатили за все эти нитки?

1. Сколько всего катушек с нитками купили?

2. Сколько денег уплатили за все эти нитки?

В настоящее время эта форма записи реше­ния задач в начальной школе практически не применяется. Однако мы считаем, что озна­комить с ней учащихся полезно и ее можно использовать на уроках математики, хотя и значительно реже, чем другие формы.

Рассмотрим другую форму записи решения той же задачи — это запись решения по дей­ствиям с пояснениями.

1. 10 · 4 =40 (коп) — стоимость белых ниток,

2. 10 ·6 = 60 (коп) — стоимость черных ни­ток.

3. 40+60=100 (коп.) — стоимость всех ни­ток.

1. 6+4 = 10 (шт.) — всего купили катушек ниток.

2. 10·10 = 100 (коп) — стоимость всех ниток.

Решение задачи можно также оформить по действиям без пояснений.

Ответ: все нитки стоят 1 руб.

Ответ: все нитки стоят 1 руб.

По задаче можно также составить выражение и найти его значение.

Ответ: все нитки стоят 1 руб

Ответ: все нитки стоят 1 руб.

Запись решения в этой форме осуществляется учащимися в два этапа. Вначале составляется выражение, затем учащиеся находят его значение, после чего запись решения приобретает вид равенства, в левой части кото­рого записано выражение, составленное по задаче, а в правой части — его значение.

Ни в коем случае нельзя называть запись 10 · 4 + 10 · 6 = 100 выражением, так как это противоречит тому определению поня­тия выражения, которое положено в основу изучения этого понятия в школе. Математи­ческое выражение составляется из цифр, букв, знаков арифметических действий и скобок, но не содержит знаков математических отноше­ний: равенства, неравенства и др. Два мате­матических выражения, соединенные знаком равенства, образуют равенство.

Приведенная выше запись — это равенство, левая часть которого есть выражение, составленное по задаче (10 · 4 + 10 ··6), а правая часть — выражение, состоящее всего лишь из одного числа (100), являющегося значением предыдущего выражения.

При проверке решения задачи, записанной в этой форме, учащимся можно дать такие задания:

1. Прочитайте выражение, составленное по задаче.

2. Назовите значение этого выражения. (Значение составленного по задаче выражения равно 100.)

3. Дайте ответ на вопрос задачи. (Все нитки стоят 100 коп., т. е. 1 руб.)

При решении задач следует правильно употреблять в своей речи соответствующие термины: Решите задачу и запишите решение по действиям с пояснениями. Решите задачу двумя способами, записав каждое решение в виде равенства, левая часть которого — выражение, составленное по задаче. Решите задачу двумя способами. Составьте соответствующие выражения и найдите их значения. Решите задачу и запишите решение вначале по действиям с пояснениями, а затем в виде выражения. Найдите значение этого выражения. Дайте ответ на вопрос задачи.

Источник

Выражения в математике.

Числовые и алгебраические выражения и их преобразования.

Как работать с математическими выражениями?

Допустим, перед вами пример. Хоть простой, хоть суперсложный (уравнение, неравенство, интеграл, производная и т.д….). Допустими, вы не Витя Перестукин и с математикой на «ты». Сможете, глядя на пример, сразу дать ответ?

В 99% случаев — нет. Если вы не гений математической мысли, конечно.)

Почему? А потому, что вам, так или иначе, придётся решать этот пример. Что значит «решать»? Это значит, последовательно, шаг за шагом, этот пример упрощать, добираясь до окончательного ответа. Или, по-другому, преобразовывать. Естественно, все эти фокусы (т.е. преобразования) надо проделывать по определённым правилам математики. Вот насколько успешно вы проведёте эти самые преобразования, настолько вы и сильны в математике.)

Так вот, имейте в виду: если вы не умеете делать правильные преобразования выражений, в математике вы не сможете сделать НИЧЕГО. Вообще ничего. Грустная перспектива? Вот и я так думаю.

Чтобы нас с вами не постигла столь печальная участь, имеет смысл разобраться в этой теме. Тем более тема достаточно простая. Разберёмся?:)

Что такое выражение в математике?

2+3 — это математическое выражение. a 2 — b 2 — это математическое выражение. И здоровенная дробь, и интеграл, и даже одно число или одна буковка — это всё математические выражения.

состоит из двух математических выражений, соединённых знаком равенства «=» (равно).

x 2 -4x+4≤0 – это тоже два математических выражения, соединённых знаком «≤» (меньше либо равно).

Короче говоря, термин «математическое выражение» применяется, чаще всего, чтобы не мычать, как корова и не кукарекать, как петух…

Спросят у вас, к примеру, что такое разность квадратов двух выражений. Первый вариант ответа: «Это ммммм… такая фиговина… Может, я лучше напишу разность? Вам какую?»

А человек в теме уверенно и с блеском в глазах ответит: «Разность квадратов двух выражений — это математическое выражение, представляющее собой произведение разности этих выражений и их суммы»!

Или: что такое квадратный корень? Квадратный корень — это математическое выражение, состоящее из подкоренного выражения и знака корня (радикала).

Согласитесь, второй вариант ответа выглядит куда более солидно и научно.)

Вот в таких вопросах фраза «математическое выражение» очень и очень удобна. Чтобы не объясняться на пальцах, как иностранные туристы в экзотической стране.

Гораздо сложнее — это конкретные математические выражения и работа с ними. Это совершенно другое дело.

Дело всё в том, что у каждого вида математических выражений имеется свой набор правил и приёмов, которому необходимо следовать при работе с ними.

У чисел — свой набор, у буквенных выражений — свой, у дробей — свой, у всяких там синусов, логарифмов, производных, интегралов — свои наборы действий. В каких-то наборах эти правила похожи или даже совпадают, а где-то — кардинально отличаются. Но пугаться этих жутких слов не надо. Эти страшные понятия мы с вами обязательно освоим в соответствующих разделах. А здесь мы с вами поработаем только с двумя видами математических выражений. А именно — с числовыми выражениями и с алгебраическими выражениями.

Что такое числовое выражение?

Что такое числовое выражение? Всё проще пареной репы.) Числовое выражение — это какое-то выражение с числами. Да-да, всего-навсего. Математическое выражение, составленное из цифр, знаков действий, скобок, знаков равенства/неравенства — это всё числовые выражения.

10-6 — числовое выражение,

(3-2,1)·0,5 — числовое выражение.

Или даже вот эти монстры:

это всё числовые выражения.

Да, в последнем примере появились специальные математические символы — радикал, значок логарифма и значок синуса. Но в этом выражении тоже нет букв. Только числа! Это самое главное.

Короче говоря, любые числа, дроби, примеры на вычисление без иксов, игреков и прочих буковок — это всё числовые выражения. Намёк понятен?)

В чём главный признак числового выражения? В том, что в нём нет букв. Вообще никаких. Математические значки (если надо) — пожалуйста. А вот букв — нету. Это ключевой признак.)

Что же можно делать с числовыми выражениями? Числовые выражения, как правило, можно (и нужно) считать. Для этого, бывает, приходится менять знаки, раскрывать скобки (или наоборот, заключать в скобки), сокращать, выносить общий множитель, раскладывать на множители т.д. То есть, делать преобразования числовых выражений. Но о преобразованиях выражений — чуть позже. Терпение, друзья.)

А здесь мы с вами разберёмся с одним забавным случаем, когда с числовым выражением делать ничего не надо. Совсем! Эта приятная операция (ничего не делать)) производится, когда числовое выражение не имеет смысла.

Понятное дело, что если мы с вами напишем какую-то белиберду типа 4+)-(=), то делать ничего и не будем. Ибо непонятно, что с этим делать. Ну, разве посчитать количество скобочек.)

Однако, попадаются в математике и внешне вполне себе благопристойные выражения.

Однако это числовое выражение тоже не имеет смысла. Почему? А потому, что если выписать отдельно знаменатель дроби да посчитать, получается ноль. На который делить нельзя. Нет такой операции в математике!

И это выражение тоже не имеет смысла! Догадались? А вы посчитайте, что под корнем получится.) Минус единичка там получится. А извлекать квадратный корень из отрицательных чисел в средней школе не учат (а вот в ВУЗе — пожалуйста). Это тоже запретное действие в (школьной) математике.

Конечно, чтобы сделать такое умозаключение, пришлось потрудиться и посчитать, что в знаменателе да под корнем получится. А в примерах может быть такого понаворочено, что… Тут уж ничего не поделаешь.)

Короче говоря, числовое выражение не имеет смысла тогда, когда в результате преобразований этого самого выражение получается запретное действие. Запретных действий в математике не так уж много: это деление на ноль, извлечение корня чётной степени из отрицательного числа, ограничения в логарифмах, в тригонометрии и в арках. Это обсуждается в соответствующих темах.

Итак, что такое числовое выражение — вникли (надеюсь).

Когда числовое выражение не имеет смысла — осознали.

Пора двигаться на следующий уровень.)

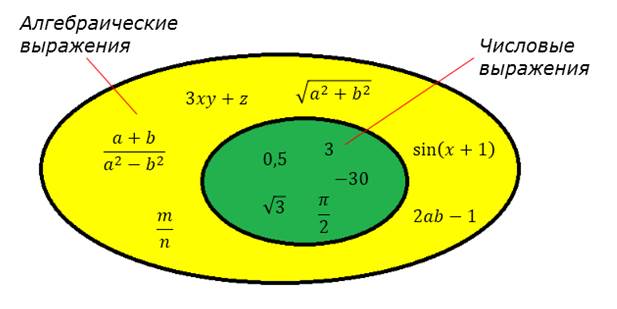
Что такое алгебраическое выражение?

Если в игру дополнительно вступают буквы, то выражение становится… Да! Оно становится алгебраическим выражением!

Понятие алгебраическое выражение — более широкое, чем числовое. Почему? Потому, что в понятие алгебраические выражения входят и все числовые тоже. То есть, любое числовое выражение — это и алгебраическое выражение. Только без букв. Типа всякий русский — россиянин, но не всякий россиянин — русский.)

В выражении х+6, например, буква икс — переменная величина. Или коротко — переменная. В отличие от шестёрки, которая — величина постоянная. Или коротко — постоянная.

Что означает термин «алгебраическое выражение»? Он означает, что, в отличие от арифметики, (которая, как известно, работает только с числами), мы должны использовать законы и правила алгебры. Непонятно? Поясняю на несложном примере:

Что можно сделать? Посчитать и всего делов-то.) Слева шестёрка и справа тоже. А для каких-нибудь других чисел такое выполняется? Тоже можно посчитать и сравнить. Но чисел в математике — бесконечное количество. И что же? Каждый раз считать и сравнивать?!

А вот если мы шагнём из арифметики в алгебру и распишем данное равенство через алгебраические выражения:

то мы сразу решим все вопросы! Для всех чисел махом! Мощная штука — алгебра.)

А когда алгебраическое выражение не имеет смысла? Что такое ОДЗ?

С числовыми выражениями всё ясно. Там на ноль делить нельзя да корни извлекать из отрицательных чисел, ну и некоторые другие логарифмические/тригонометрические фишки. А тут как узнаешь, на что делим или из чего извлекаем…

Очень просто! Точно так же!

Возьмём, к примеру, алгебраическое выражение:

Имеет ли оно смысл? Бэ-то любое число… Любое-то любое… Но есть среди этого бесконечного набора чисел такое значение b, при котором это выражение точно не имеет смысла. Догадались? Да! Это единичка (b=1). Если в знаменателе дроби заменить переменную b (как по-школьному говорят «подставить») на единичку, то в знаменателе нолик получится. На который делить нельзя. Вот и получается, что наше выражение имеет смысл при любом b, кроме единички.

И вот этот самый весь остальной набор чисел, которые можно подставлять в данное выражение, и который не приводит к запретному действию, в математике называется областью допустимых значений (ОДЗ) выражения. В нашем примере областью допустимых значений (ОДЗ) служат все числа, кроме единички.

Видим квадратный корень. Сразу соображаем (из теории, т.е. основ), что корень квадратный извлекается только из положительных чисел и нуля. А вот из отрицательных — ни в какую!

Вот и обезопасим себя вот такой записью:

Таким образом, данный хитрое выражение имеет смысл лишь при иксах, больших (или равных) двойке. Число, скажем, 3, вполне себе прокатит, а вот ноль — никак нет: он меньше двойки. ОДЗ — штука жёсткая!

Уловили принцип? Внимательно смотрим на выражение с переменными, ищем опасные места и смотрим, при каких переменных получается запретная операция. И исключаем эти значения из ОДЗ.

А потом внимательно читаем задание. Чего хотят-то? Внимательное чтение никто не отменял, да… Если в задании спрашивают, при каких значениях переменной выражение имеет смысл, то ответом будут служить все значения, кроме запретных.

Или наоборот: при каких значениях переменных выражение не имеет смысла? Тогда найденные запретные значения и будут служить ответом к заданию. Почувствуйте разницу, что называется.)

А теперь вопрос к размышлению. А зачем нам смысл выражения? Есть он, нет его… Какая разница? Дело всё в том, что это понятие становится крайне важным в старших классах! Да и в ВУЗе тоже. Без этого важного понятия вы не сможете проделывать такие простые операции, как нахождение области определения функции, ОДЗ уравнений, неравенств. Что неизбежно будет приводить к полному провалу и непониманию всех этих серьёзных тем. Увы.)

Итак, самое главное из сегодняшнего урока:

1. Числовое выражение — это выражение с числами (т.е. без букв).

2. Если, помимо чисел, в выражении есть буквы, то оно называется алгебраическим выражением.

3. Как числовое, так и алгебраическое выражение, может иметь смысл, а может и не иметь. При встрече с алгебраическим выражением первым делом ищем его ОДЗ.

4. Все допустимые значения переменной (переменных), не приводящих к запретному действию, составляют Область Допустимых Значений (ОДЗ) алгебраического выражения. При необходимости ищем её!

Ну а в различных видах преобразований выражений мы с вами подробненько разберёмся и плотно поработаем в следующих уроках этого раздела.)

Источник