Что показывает диаграмма растяжения металлов

Диаграмма растяжения (сжатия): предел пропорциональности, упругости, текучести и прочности

Автор: Константин Вавилов · Опубликовано 20.07.2015 · Обновлено 07.02.2018

Рисунок 1. Образец для испытания на растяжение

При испытании образцов на растяжение (сжатие) определяются такие характеристики как модуль упругости, коэффициент Пуассона, предел текучести, временное сопротивление и другие. Эти величины в дальнейшем используются при прочностных расчетах, расчетах на жесткость и устойчивость. Испытание образцов проводится на специальных гидравлических машинах, которые передают либо сжимающие усилия, либо растягивающие, при этом фиксируются механические характеристики испытываемых образцов. В частности, машина выводит график, показывающий зависимость между напряжениями и деформацией, либо между силой и удлинением (укорочением) образца. Такие график получил называние – диаграмма растяжения (сжатия).

Для испытания на растяжение использует образцы, представленные на рисунке 1. Отношение рабочей длины к диаметру принимается как l/d=10 либо l/d=5. Это делается для того, чтобы в разных испытательных лабораториях результаты были сравнимы.

Рисунок 2. Образец для испытания на сжатие.

Для испытания образцов на сжатие их выполняют в виде цилиндра с соотношением L/D=2. (Рисунок 2)

Для пластичных и хрупких материалов диаграммы растяжения (сжатия) несколько разнятся. Для начала рассмотрим диаграмму для пластичного материала (Рисунок 3). Примерно такую диаграмму имеют все малоуглеродистые стали (Ст2, Ст3 и т.д.)

Важные характеристики на диаграмме растяжения и сжатия

На графике по вертикали откладывается нормальное напряжение σ, по горизонтали деформация ε. Также его иногда строят в координатах сила/удлинение образца.

Пластичность – это способность материала изменять свою форму под действием внешней нагрузки и сохранять ее после снятия нагрузки.

Упругость – это способность материала искажать свою форму под действием внешней нагрузки и восстанавливать свое первоначальное состояние после ее снятия.

По достижению определенного предела напряжения график представляет собой прямую линию (Участок А-Б), то есть между напряжениями и деформациями прослеживается линейная зависимость. Таким образом, на этой участке соблюдается закон Гука:

Точка Б, до которой соблюдается это связь называется пределом пропорциональности.

Рисунок 3. Диаграмма растяжения (сжатия) малоуглеродистой стали.

Предел пропорциональности – это максимальное напряжения, при котором сохраняется пропорциональная зависимость между напряжением и деформацией.

На участке Б-В также наблюдаются упругие деформации, но материал начинает деформироваться интенсивней. Точка B соответствует пределу упругости. Не у всех материалов обнаруживается эта характеристика, поэтому чаще всего предел упругости не отмечается на диаграмме растяжения (сжатия).

Источник

Виды диаграмм растяжения

Виды диаграмм растяжения

Различные материалы по-разному ведут себя под нагрузкой, характер деформаций и разрушения зависит от типа материалов.

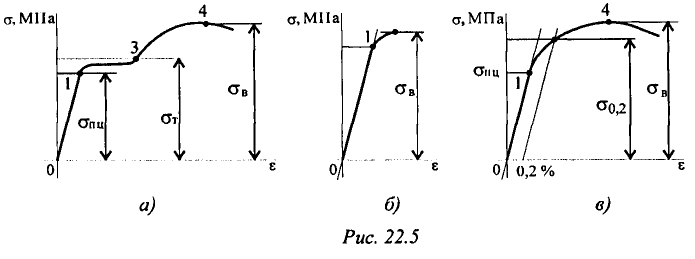
Принято делить материалы по типу их диаграмм растяжения на три группы. К первой группе относят пластичные материалы, эти материалы имеют на диаграмме растяжения площадку текучести (диаграммы первого типа) (рис. 22.5а). Ко второй группе относятся хрупкие материалы, эти материалы мало деформируются, разрушаются по хрупкому типу. На диаграмме нет площадки текучести (рис. 22.56).

К третьей группе относят материалы, не имеющие площадку текучести, но значительно деформирующиеся под нагрузкой, их называют пластично-хрупкими (рис. 22.5в).

Таким образом, хрупкий и пластично-хрупкий материалы не имеют площадки текучести, а в справочниках отсутствует характеристика «предел текучести». По этой особенности их можно узнать.

Пластично-хрупкие материалы значительно деформируются, этого нельзя допустить в работающей конструкции. Поэтому их деформацию обычно ограничивают. Максимально возможная относительная деформация 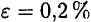. По величине максимально возможной деформации определяется соответствующее нормальное напряжение , которое принимают за предельное.

Эта теория взята со страницы решения задач по предмету «техническая механика»:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Что показывает диаграмма растяжения металлов

Диаграммы нагружения и разгружения образцов. Закон повторного нагружения

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения образца позволяет оценить поведение материала образца в упругой и упруго-пластической стадиях деформирования, определить механические характеристики материала.

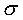
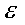
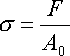
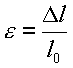
&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД ля получения численно сопоставимых между собой механических характеристик материалов диаграммы растяжения образцов перестраивают в диаграммы растяжения материалов, т.е. в зависимость между напряжением &nbsp и деформацией &nbsp, которые определяют по формулам

&nbsp&nbsp&nbsp&nbsp&nbsp,

где &nbsp- сила, действующая на образец,

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp- начальная площадь поперечного сечения и начальная длина расчетной части образца.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения материала, полученная при этих условиях (без учета изменения размеров расчетной части образца), называется условной диаграммой растяжения материала в отличие от действительной диаграммы растяжения, которую получают с учетом изменений размеров образца.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения материала зависит от его структуры, условий испытаний (температуры, скорости деформирования).

&nbsp&nbsp&nbsp

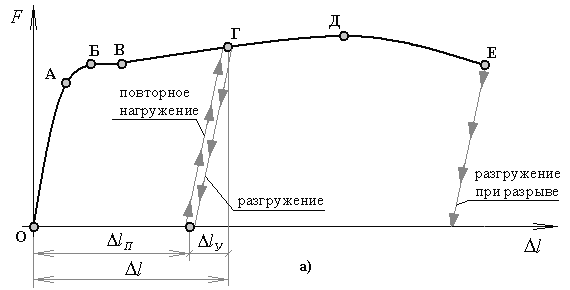
&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД иаграмма растяжения образца из низкоуглеродистой стали при однократном нагружении до разрушения. Конечная точка диаграммы соответствует разрушению.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspП ри нагружении до предела пропорциональности (точка Г диаграммы) и при дальнешем уменьшении нагрузки образец разгружается по линейному закону, который совпадает с законом первичного нагружения. В этом заключается «закон разгрузки». При нагружении образца в пределах действия закона Гука законы нагружения и последующего разгружения совпадают. При полной разгрузке образца его размеры и форма возвращаются к первоначальной кривой однократного нагружения.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbspД алее начинается участок разрушения или участок местной текучести. Он характеризуется местным утонением образца и появлянием шейки.

&nbsp&nbsp&nbsp&nbsp&nbsp &nbsp&nbsp&nbsp П ри разгружении образца в пределах участка ОА законы нагружения, разгружения и повторного нагружения совпадают.

Источник

Статическое растяжение

Статическое растяжение — одно из наиболее распространённых видов испытаний для определения механических свойств материалов.

Содержание

Основные характеристики, определяемые при испытании

При статическом растяжении, как правило, определяются следующие характеристики материала.

Основные типы материалов

Принято разделять пластичные и хрупкие материалы. Основное отличие состоит в том, что первые деформируются в процессе испытаний с образованием пластических деформаций, а вторые практически без них вплоть до своего разрушения. За критерий для условной классификации материалов можно принять относительное остаточное удлинение δ = (l_к − l₀)/l₀, где l₀ и l_к — начальная и конечная длина рабочей части образца), обычно вычисляемое в процентах. В соответствии с величиной остаточного удлинения материалы можно разделить на:

Для испытаний на статическое растяжение используют образцы как с круглым, так и с прямоугольным сечением. Предъявляются повышенные требования к изготовлению образцов, как с точки зрения геометрии, так и с точки зрения обработки резанием. Требуется высокая однородность диаметра образца по его длине, соосность и высокое качество поверхности (малая шероховатость, отсутствие царапин и надрезов). При изготовлении образцов следует избегать перегрева материала и изменений его микроструктуры.

Образцы круглого сечения, как правило, имеют рабочую длину, равную четырём или пяти диаметрам — т. н. короткие образцы или десяти диаметрам — т. н. нормальные образцы. Перед началом испытания замеряется диаметр образца (обычно 6, 10 или 20 мм) для вычисления напряжения σ и для расчёта относительного остаточного сужения после разрушения образца. В случае использования экстензометра, длина рабочей части образца не замеряется, а деформация ε и относительное удлинение при разрушении регистрируются автоматически с помощью компьютера или измеряются по диаграмме σ — ε. При отсутствии экстензометра (не рекомендуется стандартом), отмечается рабочая длина образца, деформация ε рассчитывается по перемещениям конца образца (захвата), а относительное удлинение при разрушении рассчитывается путём замера разрушенного образца.

Диаграмма растяжения пластичного материала

Обычно диаграмма растяжения является зависимостью приложенной нагрузки P от абсолютного удлинения Δl. Современные машины для механических испытаний позволяют записывать диаграмму в величинах напряжения σ (σ = P/A₀, где A₀ — исходная площадь поперечного сечения) и линейной деформации ε (ε = Δl/l₀ ). Такая диаграмма носит название диаграммы условных напряжений, так как при этом не учитывается изменение площади поперечного сечения образца в процессе испытания.

Начальный участок является линейным (т. н. участок упругой деформации). На нём действует закон Гука:

Затем начинается область пластической деформации. Эта деформация остаётся и после снятия приложенной нагрузки. Переход в пластическую область обнаруживается не только по проявлению остаточных деформаций, но и по уменьшению наклона кривой с увеличением степени деформации. Данный участок диаграммы обычно называют площадкой (зоной) общей текучести, так как пластические деформации образуются по всей рабочей длине образца. С целью изучения и точного анализа диаграммы деформации, современные испытательные машины оснащены компьютеризированной записью результатов.

По наклону начального участка диаграммы рассчитывается модуль Юнга. Для малоуглеродистой стали наблюдается т. н. «зуб текучести» и затем площадка предела текучести. Явление «зуба» текучести связано с дислокационным механизмом деформации. На начальном участке плотность дислокаций является недостаточной для обеспечения более высокой степени деформации. После достижения точки верхнего предела текучести начинается интенсивное образование новых дислокаций, что приводит к падению напряжения. Дальнейшая деформация при пределе текучести происходит без роста напряжения . Зависимость предела текучести, от размера зерна, d, выражена соотношением Холла-Петча:

После достижения конца площадки текучести (деформация порядка 2 — 2,5 %) начинается деформационное упрочнение (участок упрочнения), видимое на диаграмме, как рост напряжения с ростом деформации. В этой области до достижения максимальной нагрузки (напряжения (σ_В) макродеформация остаётся равномерной по длине испытуемого образца. После достижения точки предела прочности начинает образовываться т. н. «шейка» — область сосредоточенной деформации. Расположение «шейки» зависит от однородности геометрических размеров образца и качества его поверхности. Как правило, «шейка» и, в конечном счёте, место разрушения расположено в наиболее слабом сечении. Кроме того, важное значение имеет одноосность напряжённого состояния (отсутствие перекосов образца в испытательной машине). Для пластичных материалов при испытании на статическое растяжение одноосное напряжённое состояние сохраняется лишь до образования т. н. «шейки» (до достижения максимальной нагрузки и начала сосредоточенной деформации).

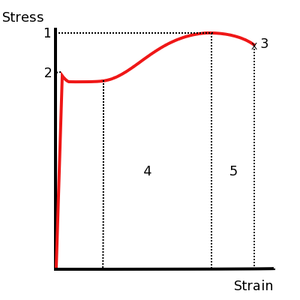
Вид диаграммы деформации, приведённый на рис. 1 является типичным для О.Ц.К. материалов с низкой исходной плотностью дислокаций.

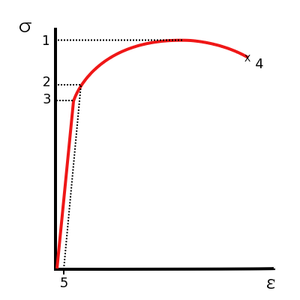
Для многих материалов, например, с Г. Ц. К. кристаллической решёткой, а также для материалов с высокой исходной плотностью дефектов, диаграмма имеет вид, показанный на рис. 2. Основное отличие — отсутствие явно выраженного предела текучести. В качестве предела текучести выбирается значение напряжения при остаточной деформации 0,2 % (σ_0.2).

После достижения максимума нагрузки происходит падение нагрузки (и, соответственно, напряжения σ) за счёт локального уменьшения площади поперечного сечения образца. Соответствующий (последний) участок диаграммы называют зоной местной текучести, так как пластические деформации продолжают интенсивно развиваться только в области шейки.

Иногда используется диаграмма истинных напряжений, S — e (истинное напряжение S = P/A, где A — текущая площадь поперечного сечения образца; истинная деформация e = Δl/l, где l — текущая длина образца). В этом случае, после достижения максимальной нагрузки не происходит падения напряжения, истинное напряжение растёт за счёт локального уменьшения сечения в «шейке» образца. Поэтому различие между диаграммами истинных и условных напряжений наблюдается только после предела прочности — до точки 1 они практически совпадают друг с другом.

Образцы из пластичного материала разрушаются по поперечному сечению с уменьшением диаметра в месте разрыва из-за образования «шейки».

Диаграмма растяжения хрупкого материала

Диаграмма растяжения и диаграмма условных напряжений хрупких материалов по виду напоминает диаграмму, показанную на рис. 2 за тем исключением, что не наблюдается снижения нагрузки (напряжения) вплоть до точки разрушения. Кроме того, данные материалы не получают таких больших удлинений как пластичные и по времени разрушаются гораздо быстрее. На диаграмме хрупких материалов уже на первом участке имеется ощутимое отклонение от прямолинейной зависимости между нагрузкой и удлинением (напряжением и деформацией), так что о соблюдении закона Гука можно говорить достаточно условно. Так как пластических деформаций хрупкий материал не получает, то в ходе испытания не определяют предела текучести. Не имеет особенного смысла также рассчитывать и относительное сужение образца, так как шейка не образуется и диаметр после разрыва практически не отличается от исходного.

Влияние скорости деформации и температуры на прочностные характеристики

Стандарты на проведение испытаний на статическое растяжение, как правило, ограничивают скорость деформации или скорость приложения нагрузки. Так, стандарт ASTM E-8 ограничивает скорость деформации величиной 0,03 — 0,07 мм/мин. Такое ограничение вызвано искажением результатов за счёт повышения прочности металлов с ростом скорости деформации (при постоянной температуре). При скоростях деформации до 1 сек скорость деформации практически не влияет на прочностные характеристики (в частности, на предел текучести).

В общем виде можно выразить формулу влияния скорости деформации на предел текучести в виде:

где — скорость деформации; — астотный фактор, — активационный объём; — напряжение течения; — экстраполяция напряжения течения на нулевую скорость деформации.

Эта же зависимость даёт и зависимость напряжения течения от температуры. В области низких температур и при отсутствии фазовых превращений прочность кристаллических материалов повышается. Вклад в повышение прочности даёт и переход от термически активируемого процесса деформации за счёт движения дислокаций к механизму деформации путём двойникования.

Источник

Диаграмма растяжения металлов.

При статических испытаниях на растяжение определяют вели­чины, характеризующие прочность, пластичность и упругость мате­риала. Испытания производятся на цилиндрических (или плоских) образцах с определенным соотношением между длиной l₀ и диа­метром d₀. Образец растягивается под действием приложенной силы Р (рис. 1, а) до разрушения. Внешняя нагрузка вызывает в образце напряжение и деформацию. Напряжение σ — это отношение силы Р к площади поперечного сеченияF₀, МПа:

Деформация характеризует изменение размеров образца под дей­ствием нагрузки, %:

где l₁ — длина растянутого образца.

Деформация может быть упру­гой (исчезающей после снятия нагрузки) и пластической (остаю­щейся после снятия нагрузки).

После проведения ис­пытаний определяются следующие характеристики механических свойств.

Предел упругостиσ_у— это максимальное напряжение при кото­ром в образце не возникают пластические деформации.

Предел текучестиσ_т— это напряжение, соответствующее площадке текучести на диаграмме растяжения (рис. 1). Если на диаграмме нет площадки текучести(что наблюдается для хрупких материалов), то определяют условный предел текучести σ_0,2— напряжение, вызывающее пластическую деформацию, равную 0,2 %. Предел прочности (или временное сопротивление) σ_в— это на­пряжение, отвечающее максимальной нагрузке, которую выдержи­вает образец при испытании.

Относительное удлинение после разрыва δ— отношение при­ращения длины образца при растяжении к начальной длине l₀, %:

где l_к — длина образца после разрыва.

Относительным сужением после разрыва ψ называется умень­шение площади поперечного сечения образца, отнесенное к началь­ному сечению образца, %:

где F_к — площадь поперечного сечения образца в месте разрыва. Относительное удлинение и относительное сужение характеризуют пластичность материала.

Рис. 1. Статические испытания на растяжение: а – схема испытания;

б – диаграмма растяжения

Твердость– это сопротивление материала проникновению в его поверхность стандартного тела (индентора), не деформирующегося при испытании.

Широкое распространение объясняется тем, что не требуются специальные образцы.

Это неразрушающий метод контроля. Основной метод оценки качества термической обработке изделия. О твердости судят либо по глубине проникновения индентора (метод Роквелла), либо по величине отпечатка от вдавливания (методы Бринелля, Виккерса, микротвердости).

Во всех случаях происходит пластическая деформация материала. Чем больше сопротивление материала пластической деформации, тем выше твердость.

Наибольшее распространение получили методы Бринелля, Роквелла, Виккерса и микротвердости.

Рис. 7.1. Схемы определения твердости: а – по Бринеллю; б – по Роквеллу;

Твердость по Бринеллю ( ГОСТ 9012)

Метод Бринелля основан на вдавливании в поверхность металла стального закаленного шарика под действием определенной нагрузки. После снятия нагрузки в образце остается отпечаток. Полученный отпечаток измеряется в двух направлениях при помощи лупы Бринелля.

Твердость определяется как отношение приложенной нагрузки Р к сферической поверхности отпечатка F:

Стандартными условиями являются D = 10 мм; Р = 3000 кгс; = 10 с. В этом случае твердость по Бринеллю обозначается НВ 250, в других случаях указываются условия: НВ D / P / , НВ 5/ 250 /30 – 80.

Метод Роквелла ГОСТ 9013

Метод Роквелла основан на вдавливании в испытуемый образец закаленного стального шарика диаметром 1,6 мм (шкала В) или алмазного конуса с углом при вершине 120° (шкалыА и С). Вдавли­вание производится под действием двух нагрузок — предваритель­ной равной 100 Н и окончательной равной 600, 1000. 1500 Н для шкалА, В и С соответственно. Число твердости по РоквеллуHRA, HRB и HRC определяется по разности глубин вдавливания.

Индентор для мягких материалов (до НВ 230) – стальной шарик диаметром 1/16” ( 1,6 мм), для более твердых материалов – конус алмазный.

Нагружение осуществляется в два этапа. Сначала прикладывается предварительная нагрузка (10 ктс) для плотного соприкосновения наконечника с образцом. Затем прикладывается основная нагрузка Р₁, в течение некоторого времени действует общая рабочая нагрузка Р. После снятия основной нагрузки определяют значение твердости по глубине остаточного вдавливания наконечника h под нагрузкой .

В зависимости от природы материала используют три шкалы твердости (табл. 7.1)

Таблица 7.1.Шкалы для определения твердости по Роквеллу

Метод Виккерса

В методе Виккерса применяют вдавливание алмазной четырех­гранной пирамиды с углом при вершине 136°. Число твердости по ВиккерсуHV определяется отношением приложенной нагрузки к площади поверхности отпечатка.

Твердость рассчитывается как отношение приложенной нагрузки P к площади поверхности отпечатка F:

Нагрузка Р составляет 5…100 кгс. Диагональ отпечатка d измеряется при помощи микроскопа, установленного на приборе.

Преимущество данного способа в том, что можно измерять твердость любых материалов, тонкие изделия, поверхностные слои. Высокая точность и чувствительность метода.

В результате проведения динамических испытаний на ударный изгиб специальных образцов с надрезом (ГОСТ 9454) оценивается вязкость материалов и устанавливается их склонность к переходу из вязкого состояния в хрупкое.

Вязкость – способность материала поглощать механическую энергию внешних сил за счет пластической деформации.

Является энергетической характеристикой материала, выражается в единицах работы Вязкость металлов и сплавов определяется их химическим составом, термической обработкой и другими внутренними факторами.

Также вязкость зависит от условий, в которых работает металл (температуры, скорости нагружения, наличия концентраторов напряжения).

Способы оценки вязкости.

Ударная вязкость определяется работой A, затраченной на разрушение образца, отнесенной к площади его поперечною сече­ния F; Дж/м2:

Ударная вязкость характеризует надежность материала, его способность сопротивляться хрупкому разрушению

Рис.7.3. Схема испытания на ударную вязкость: а – схема маятникового копра;

На разрушение образца затрачивается работа:

где: Р – вес маятника, Н – высота подъема маятника до удара, h – высота подъема маятника после удара.

где: F₀ — площадь поперечного сечения в месте надреза.

Лекция 4

Дата добавления: 2018-06-27 ; просмотров: 989 ; Мы поможем в написании вашей работы!

Источник