Что общего в записи координат каждой группы точек
§ 6. Координатная плоскость
6.1. Назовите абсциссу и ординату точки:
Не производя построения, ответьте на вопрос, в каком координатном угле расположена точка:
6.3. Замените символ * каким-либо числом так, чтобы:
Не производя построения, ответьте на вопрос, в каком координатном угле координатной плоскости хОу расположена точка:
6.4. а) А(а; 10), если а > 0;
б) В(17; b), если b 0;
г) D(-8; d), если d 0, y > 0;
б) Q(x; у), если х > 0, у 0;
г) S(x; у), если х 0, b 0;
г) L(-a; b), если а > 0, b > 0?
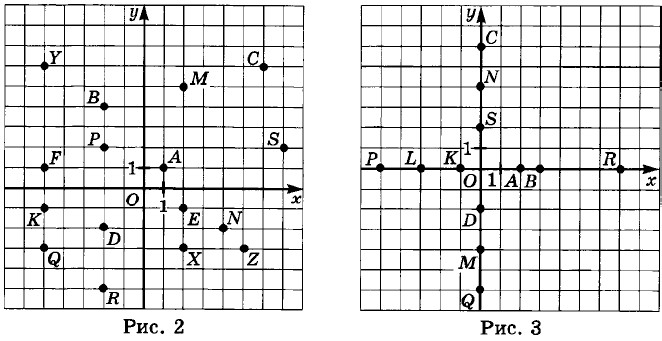
6.7. Найдите координаты точек, изображённых на рис. 2:
а) А, С, М, S;
б) R, D, К, Q;
в) Р, У, В, F;
г) Е, N, X, Z.
Какой признак объединяет каждую группу точек?
6.8. Найдите координаты точек, изображённых на рис. 3:
а) А, В, К, Р, L, R; б) С, D, М, N, Q, S.
Какой общий графический признак объединяет эти точки?
Как этот общий признак выражается при записи координат точек?
в) Где расположены все точки, у которых абсцисса равна нулю; ордината равна нулю?
г) Составьте аналитическую модель множества точек, лежащих на оси х; на оси у.
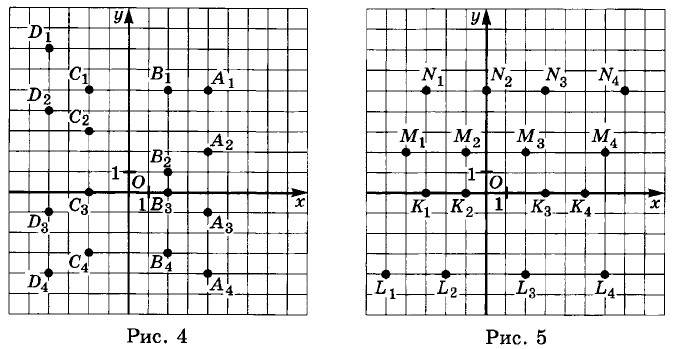
6.9. Найдите координаты точек, изображённых на рис. 4.
Что общего в записи координат каждой группы точек?
Как расположены на координатной плоскости все точки, имеющие одинаковую абсциссу?
Составьте аналитическую модель прямой, параллельной оси у.
6.10. Найдите координаты точек, изображённых на рис. 5.
Что общего в записи координат каждой группы точек?
Как расположены на координатной плоскости все точки, имеющие одинаковую ординату?
Составьте аналитическую модель прямой, параллельной оси х.
Как найти координаты точки?
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
Определение координат точки
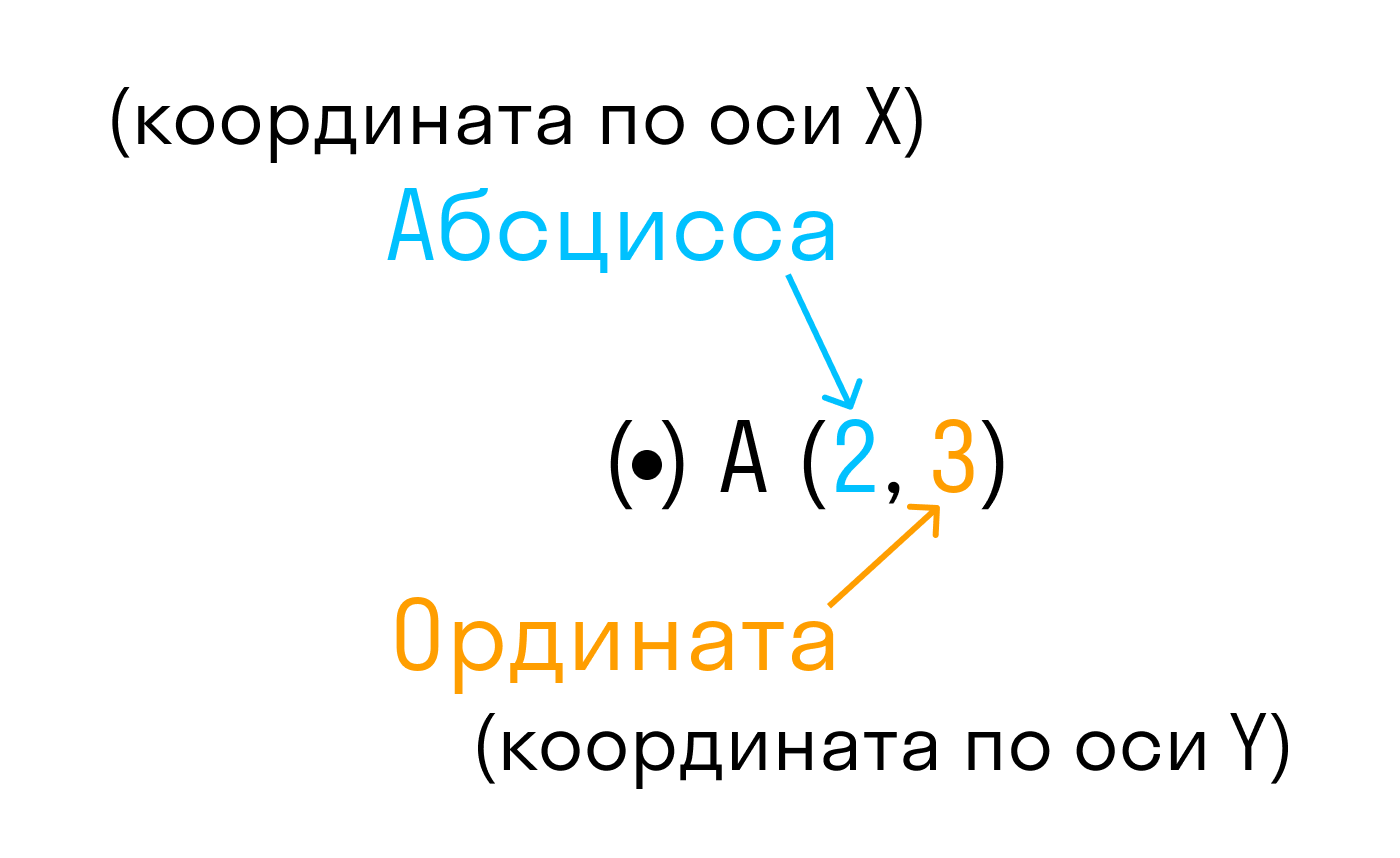
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
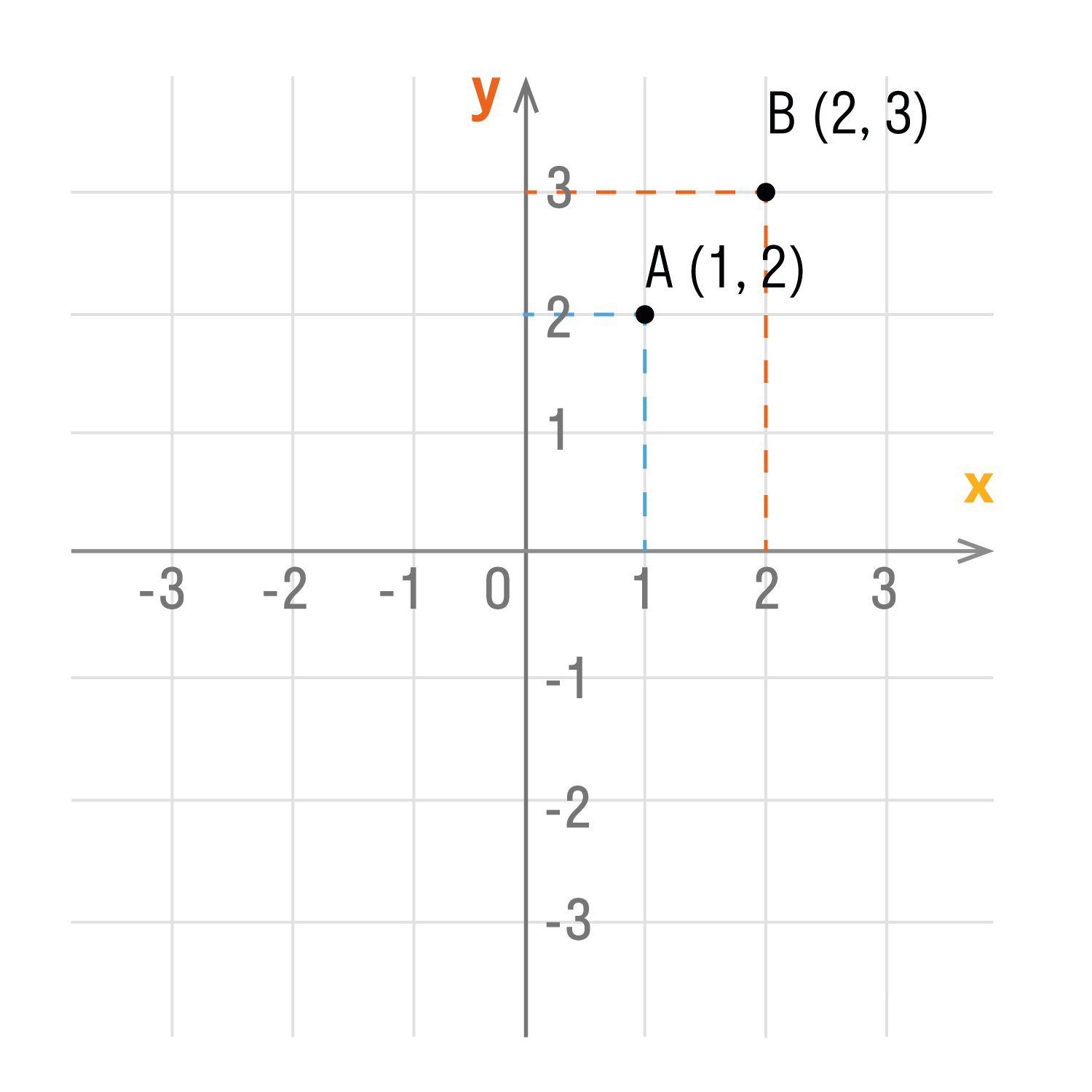
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
Способ второй. Как определить положение точки D (-4, 2):
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике: