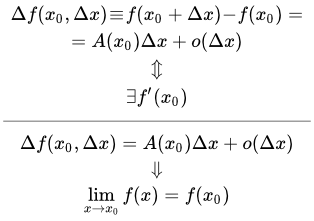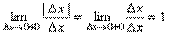Что означает понятие дифференцированная функция

Дифференцируемые функции в точке – определение и свойства

Определение дифференцируемой функции

Как мы увидим ниже, определение дифференцируемой функции одной переменной эквивалентно существованию ее производной. Тогда возникает вопрос – почему нельзя сразу дать определение, что дифференцируемая функция – это функция, имеющая производную?

Ответ на этот вопрос раскрывается при рассмотрении функций нескольких переменных. Дело в том, что производные вычисляются только от функций, зависящих от одной переменной. Для функций двух и более переменных, вначале выбирают направление приближения к заданной точке (например, ось x или ось y ), а затем по этому направлению вычисляют производную. Поэтому в любой точке имеется бесконечное множество производных по различным направлением. Из-за этого производные не фигурируют в определении дифференцируемой функции.

Свойства дифференцируемой функции

Таким образом, в случае функции от одной переменной, дифференцируемость функции в точке эквивалентно существованию производной в этой точке. Забегая вперед укажем, что в случае функций многих переменных, для того чтобы функция была дифференцируемой в точке, необходимо, чтобы она имела в этой точке частные производные, и достаточно, чтобы она имела в этой точке непрерывные частные производные.

Доказательства теорем

Связь дифференцируемости функции с существованием производной

В нашем случае это означает, что
.
Отсюда
.

Связь дифференцируемости функции с ее непрерывностью

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Дифференцируемая функция

Из Википедии — свободной энциклопедии

Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. Дифференцируемость является одним из фундаментальных понятий в математике и имеет значительное число приложений как в самой математике, так и в других естественных науках.

Приращение дифференцируемой в данной точке функции можно представить как линейную функцию приращения аргумента с точностью до величин более высокого порядка малости. Это означает, что для достаточно малых окрестностей данной точки функцию можно заменить линейной (скорость изменения функции можно считать неизменной). Линейная часть приращения функции называется её дифференциалом (в данной точке).

Необходимым, но не достаточным условием дифференцируемости является непрерывность функции. В случае функции от одной вещественной переменной дифференцируемость равносильна существованию производной. В случае функции нескольких вещественных переменных необходимым (но не достаточным) условием дифференцируемости является существование частных производных по всем переменным. Для дифференцируемости функции нескольких переменных в точке достаточно, чтобы частные производные существовали в некоторой окрестности рассматриваемой точки и были непрерывны в данной точке. [1]

В случае функции комплексной переменной дифференцируемость в точке часто называется моногенностью и существенно отличается от понятия дифференцируемости в вещественном случае. Ключевую роль в этом играет так называемое условие Коши — Римана. Функция, моногенная в окрестности точки, называется голоморфной в этой точке. [2] [3]

В функциональном анализе существует обобщение понятия дифференцирования на случай отображений бесконечномерных пространств — производные Гато и Фреше.

Обобщением понятия дифференцируемой функции являются понятия субдифференцируемых, супердифференцируемых и квазидифференцируемых функций.

Источник

Дифференцирование функции, нахождение производной

Если вам нужно решить задачу, в рамках которой требуется вычислить производную какой-либо функции с одной переменной, советуем внимательно прочесть эту статью. Здесь приводятся общие положения теории дифференцирования, имеющие отношение к вычислению производной. Для этого могут быть использованы разные способы, ведь исходная функция может быть задана явно или неявно, в параметрическом виде, быть элементарной, основной или сложной, значит, в каждой ситуации бывает нужен свой подход.

Таблица дифференцирования функции

Мы собрали всю информацию, которую нужно знать для правильного дифференцирования функции, и представили ее в табличном виде:

Степенная фунция y = x p

y = a x a x ‘ = a x · ln a

В частности, при a = e имеем

log a x ‘ = 1 x · ln a

В частности, при a = e имеем

y = ln x ln x ‘ = 1 x

Производная сложной функции

( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x )

Производная неявно заданной функции

Производная обратной функции

Обратные тригонометрические функции

Производная параметрически заданной функции

y = f ( x ) y ‘ = y · ( ln ( f ( x ) ) ) ‘

Пояснения таблицы

Содержимое таблицы требует небольших пояснений. Например, в наиболее простом случае для дифференцирования нам пригодится определение производной, т.е. вычисление соответствующего предела. Это действие носит название непосредственного дифференцирования.

Если вам приходится работать с основной элементарной функцией, то следует использовать таблицу основных производных. В ней приводятся все готовые значения, доказанные на основании определения. Это очень удобно, и мы советуем вам держать такую таблицу под рукой.

Источник

В более общем плане для Икс₀ как внутреннюю точку области определения функции ж, тогда ж как говорят дифференцируемый в точке x₀ тогда и только тогда, когда производная ж ′(Икс₀) существуют. Другими словами, график ж имеет невертикальную касательную в точке (Икс₀, ж(Икс₀)). Функция ж также называется локально линейный в Икс₀ поскольку это хорошо аппроксимируется линейная функция рядом с этой точкой.

Содержание

Дифференцируемость действительных функций одной переменной

Дифференцируемость и преемственность

Большинство функций, которые встречаются на практике, имеют производные во всех точках или в почти каждый точка. Однако в результате Стефан Банах утверждает, что набор функций, имеющих производную в некоторой точке, является скудный набор в пространстве всех непрерывных функций. [1] Неформально это означает, что дифференцируемые функции очень нетипичны среди непрерывных функций. Первым известным примером функции, непрерывной всюду, но нигде не дифференцируемой, является функция Функция Вейерштрасса.

Классы дифференцируемости

Функция ж как говорят непрерывно дифференцируемый если производная ж ′ (Икс) существует и сама является непрерывной функцией. Хотя производная дифференцируемой функции никогда не имеет скачкообразный разрыв, производная может иметь существенный разрыв. Например, функция

дифференцируема в 0, так как

существуют. Однако для Икс ≠ 0, правила дифференциации подразумевать

который не имеет предела как Икс → 0. Тем не менее, Теорема Дарбу означает, что производная любой функции удовлетворяет заключению теорема о промежуточном значении.

Дифференцируемость в высших измерениях

Однако существование частных производных (или даже всех производные по направлению), вообще говоря, не гарантирует дифференцируемости функции в точке. Например, функция ж: р 2 → р определяется

Дифференцируемость в комплексном анализе

Любая функция, комплексно-дифференцируемая в окрестности точки, называется голоморфный в таком случае. Такая функция обязательно бесконечно дифференцируема, и на самом деле аналитический.

Дифференцируемые функции на многообразиях

Если M это дифференцируемое многообразие, действительная или комплексная функция ж на M называется дифференцируемой в точке п если она дифференцируема относительно некоторой (или любой) координатной карты, определенной вокруг п. В более общем смысле, если M и N дифференцируемые многообразия, функция ж: M → N называется дифференцируемой в точке п если она дифференцируема относительно некоторых (или любых) координатных карт, определенных вокруг п и ж(п).

Источник

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ.

Функция y=f(x) называется дифференцируемой в некоторой точке x₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

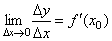
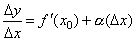
Доказательство. Если , то ,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда

Таким образом,из дифференцируемости функции следует ее непрерывность.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

Рассмотрим на рисунке точки а, b, c.

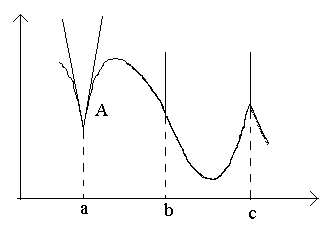
В точке a при Δx→0 отношение не имеет предела (т.к. односторонние пределы различны при Δx→0–0 и Δx→0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к₁ и к₂. Такой тип точек называют угловыми точками. В точке b при Δx→0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – «точка перегиба» c вертикальной касательной.

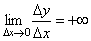
В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.

Пример.

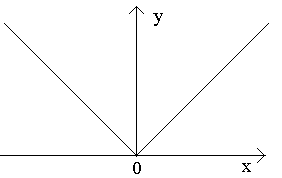
Покажем, что она не имеет производной в этой точке.

Т.о., отношение при Δx→ 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x| в точке x= 0 не существует. Геометрически это значит, что в точке x= 0 данная «кривая» не имеет определенной касательной (в этой точке их две).

Источник