Что означает решить неравенство
Решение линейных неравенств
Основные понятия
Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.
Линейные неравенства — это неравенства вида:
где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти все значения переменной, при которой неравенство верное.
Типы неравенств
Линейные неравенства: свойства и правила
Вспомним свойства числовых неравенств:
Если же а b и c > d, то а + c > b + d.
Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.
Если а d, то а – c b, m — положительное число, то mа > mb и
Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).
Если же а > b, n — отрицательное число, то nа
Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.
Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>
Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.
Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.
Свойства выше помогут нам использовать следующие правила.
Правила линейных неравенств
Решение линейных неравенств
Линейные неравенства с одной переменной x выглядят так:
где a и b — действительные числа. А на месте x может быть обычное число.
Равносильные преобразования
Рассмотрим пример: 0 * x + 5 > 0.
Как решаем:
Метод интервалов
Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.
Метод интервалов заключается в следующем:
Если a ≠ 0, тогда решением будет единственный корень — х₀;
Для этого найдем значения функции в точках на промежутке;
Как решаем:
В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,
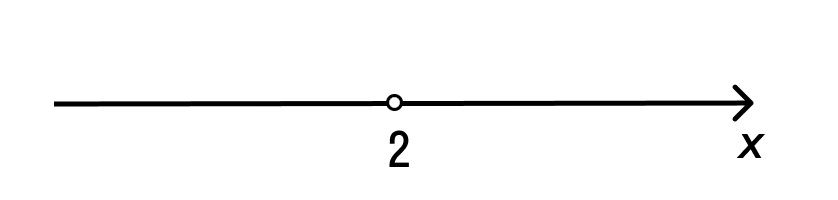
Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.
Определим знаки на промежутках.
Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.
Графический способ
Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.
Алгоритм решения y = ax + b графическим способом
Рассмотрим пример: −5 * x − √3 > 0.
Как решаем
Ответ: (−∞, −√3 : 5) или x
Решение неравенств
Определение и формулы неравенств
Знаки > называются знаками строгого неравенства, а знаки 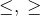
Если в неравенство входят только числовые величины, то такое неравенство называется числовым неравенством.
Решить неравенство — это значит найти множество всех его решений
Неравенства называют равносильными, если они имеют одно и тоже множество решений.
Основные правила, применяемые при решении неравенств
Если требуется все общие решения двух или нескольких неравенств, то решают систему неравенств. Как и систему уравнений, систему неравенств записывают с помощью фигурной скобки. Решение системы неравенств есть пересечение решений всех входящих в нее неравенств.
Одним из основных методов решения неравенств является метод интервалов.
Примеры решения неравенств
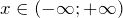
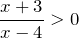
Решим каждую систему неравенств отдельно: 2. Объединим полученные решения и запишем решение исходного неравенства Прежде чем перейти к определению и решению неравенств давайте вспомним, какие знаки используют в математике для сравнения величин. Теперь мы можем разобраться, что называют линейным неравенством и чем неравенство отличается от уравнения. В отличии от уравнения в неравенстве вместо знака равно « = » используют любой знак сравнения: « > », « », « ≤ » или « ≥ ». Линейным неравенством называют неравенство, в котором неизвестное стоит только в первой степени. Рассмотрим пример линейного неравенства. Чтобы решить неравенство, нужно чтобы в левой части осталось только неизвестное в первой степени с коэффициентом « 1 ». При решении линейных неравенств используют правило переноса и правило деления неравенства на число. Также как и в уравнениях, в неравенствах можно переносить любой член неравенства из левой части в правую и наоборот. Вернемся к нашему неравенству и используем правило переноса. Для того, чтобы понять, что получается при решении неравенства, нам нужно вспомнить, понятие числовой оси. Нарисуем числовую ось для неизвестного « x » и отметим на ней число « 14 ». При нанесении числа на числовую ось соблюдаются следующие правила: Заштрихуем на числовой оси по полученному ответу « x » все решения неравенства, то есть область слева от числа « 14 ». Рисунок выше говорит о том, что любое число из заштрихованной области при подстановке в исходное неравенство « x − 6 » даст верный результат. Возьмем, например число « 12 » из заштрихованной области и подставим его вместо « x » в исходное неравенство « x − 6 ». Другими словами, можно утверждать, что любое число из заштрихованной области будет являться решением неравенства. Решить неравенство — это значит найти множество чисел, которые при подстановке в исходное неравенство дают верный результат. Решением неравенства называют множество чисел из заштрихованной области на числовой оси. В нашем примере ответ « x » можно понимать так: любое число из заштрихованной области (то есть любое число меньшее « 14 ») будет являться решением неравенства « x − 6 ». Рассмотрим другое неравенство. Используем правило переноса и перенесём все числа без неизвестного, в правую часть. Теперь нам нужно сделать так, чтобы при неизвестном « x » стоял коэффициент « 1 ». Для этого достаточно разделить и левую, и правую часть на число « 2 ». При умножении или делении неравенства на число, на это число умножается (делится) и левая, и правая часть. Разделим « 2x > 16 » на « 2 ». Так как « 2 » — положительное число, знак неравенства останется прежним. Рассмотрим другое неравенство. Разделим неравенство на « −3 ». Так как мы делим неравенство на отрицательное число, знак неравенства поменяется на противоположный. Статья находится на проверке у методистов Skysmart. Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения. Решение — значение переменной, при котором неравенство становится верным. Решить неравенство значит найти множество, для которых оно выполняется. Квадратное неравенство выглядит так: Квадратное неравенство можно решить двумя способами: При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения. Как дискриминант влияет на корни уравнения: Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств. Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +. Если неравенство со знаком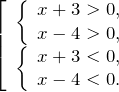
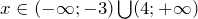
Решение линейных неравенств
Символ Название Тип знака > больше строгий знак
(число на границе не включается )строгий знак
(число на границе не включается )≥ больше или равно нестрогий знак
(число на границе включается )≤ меньше или равно нестрогий знак
(число на границе включается )Как решить линейное неравенство
Правило переноса в неравенствах
Правило умножения или деления неравенства на число
Метод интервалов, решение неравенств
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).Определение квадратного неравенства
Решение неравенства графическим методом
Решение неравенства методом интервалов

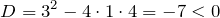







 равносильны по теореме 1. Неравенства
равносильны по теореме 1. Неравенства  и
и  равносильны по теореме 2 (обе части
равносильны по теореме 2 (обе части
 (рис. 1.113).
(рис. 1.113).
 расположен выше графика функции
расположен выше графика функции  при х > 2.
при х > 2.
 (или соответственно
(или соответственно  ). Если
). Если  , то неравенство
, то неравенство  равносильно неравенству
равносильно неравенству  (см. теорему 2); значит, множество решений неравенства есть промежуток
(см. теорему 2); значит, множество решений неравенства есть промежуток  . Если
. Если  , то неравенство
, то неравенство  равносильно неравенству
равносильно неравенству  (см. теорему 3); значит, множество решений неравенства есть промежуток
(см. теорему 3); значит, множество решений неравенства есть промежуток  . Если
. Если  , то неравенство принимает вид
, то неравенство принимает вид  ; оно не имеет решений, если
; оно не имеет решений, если  , и верно при любых х, если b З и Зх-2 может быть и любой другой знак неравенства), где р(х) и q(x) — многочлены, основано на следующем рассуждении.
, и верно при любых х, если b З и Зх-2 может быть и любой другой знак неравенства), где р(х) и q(x) — многочлены, основано на следующем рассуждении. , где
, где  Если х > d, то каждый из множителей
Если х > d, то каждый из множителей  положителен и, следовательно, на промежутке
положителен и, следовательно, на промежутке  имеем h(x) > 0. Если с 0 и т. д. (рис. 1.124).
имеем h(x) > 0. Если с 0 и т. д. (рис. 1.124). , неравенство
, неравенство  равносильно неравенству противоположного смысла f(х) g(x). В случае же, когда
равносильно неравенству противоположного смысла f(х) g(x). В случае же, когда  , от исходного неравенства следует перейти к неравенству противоположного смысла f(х) 0 и g(x) > 0.
, от исходного неравенства следует перейти к неравенству противоположного смысла f(х) 0 и g(x) > 0. при
при  равносильно системе неравенств
равносильно системе неравенств





 , то данное неравенство можно переписать в виде
, то данное неравенство можно переписать в виде 
 Далее имеем
Далее имеем







 (1)
(1) и решением неравенства g(x) > 0 (из неравенства (1) следует, что
и решением неравенства g(x) > 0 (из неравенства (1) следует, что  ). Значит, неравенство (1) равносильно системе неравенств
). Значит, неравенство (1) равносильно системе неравенств

 равносильно системе неравенств
равносильно системе неравенств
 (2)
(2) , но в отличие от предыдущего случая здесь g(x) может принимать как неотрицательные, так и отрицательные значения. Поэтому заданное неравенство (2) рассмотрим в каждом из следующих случаев: g(x) 0.
, но в отличие от предыдущего случая здесь g(x) может принимать как неотрицательные, так и отрицательные значения. Поэтому заданное неравенство (2) рассмотрим в каждом из следующих случаев: g(x) 0. (рис. 1.129), а всего таких интервалов будет бесконечно много,
(рис. 1.129), а всего таких интервалов будет бесконечно много,
 Таким образом, решением заданного неравенства служит объединение интервалов вида
Таким образом, решением заданного неравенства служит объединение интервалов вида  Это можно записать так:
Это можно записать так:

 Нас интересуют те значения аргумента х, которым соответствуют точки графика, лежащие ниже прямой
Нас интересуют те значения аргумента х, которым соответствуют точки графика, лежащие ниже прямой  Одним из нужных нам промежутков является интервал
Одним из нужных нам промежутков является интервал  (рис. 1.130).
(рис. 1.130).

 .
.
 (рис. 1.131), а всего таких промежутков будет бесконечно много, причем в силу периодичности функции у = tg х каждый получается из
(рис. 1.131), а всего таких промежутков будет бесконечно много, причем в силу периодичности функции у = tg х каждый получается из  Это позволяет записать решение следующим образом:
Это позволяет записать решение следующим образом:



 . Построим на координатной плоскости параболу — график функции
. Построим на координатной плоскости параболу — график функции  .
. , больше, чем ордината точки, имеющей ту же абсциссу, но лежащей на параболе, и так как неравенство
, больше, чем ордината точки, имеющей ту же абсциссу, но лежащей на параболе, и так как неравенство  нестрогое, то геометрическим изображением решений заданного неравенства будет множество точек плоскости, лежащих на параболе
нестрогое, то геометрическим изображением решений заданного неравенства будет множество точек плоскости, лежащих на параболе 
 и
и  обозначает на плоскости некоторую линию, можно сказать, что неравенство с двумя переменными
обозначает на плоскости некоторую линию, можно сказать, что неравенство с двумя переменными  обозначается множество точек плоскости, координаты которых удовлетворяют этому неравенству. Таким образом геометрически толковать и неравенство
обозначается множество точек плоскости, координаты которых удовлетворяют этому неравенству. Таким образом геометрически толковать и неравенство 
 является линейным, то есть
является линейным, то есть  где
где 
 — постоянные, то мы получим линейное уравнение
— постоянные, то мы получим линейное уравнение

 и границей которой прямая
и границей которой прямая  Проверить, лежит в этой же полуплоскости начало координат.
Проверить, лежит в этой же полуплоскости начало координат. в левую часть уравнения заданной прямой:
в левую часть уравнения заданной прямой:  Полученная величина положительна. Следует, точка
Полученная величина положительна. Следует, точка 




 можно рассмотреть как пересечение трех полуплоскостей, из которых первая ограничена прямой
можно рассмотреть как пересечение трех полуплоскостей, из которых первая ограничена прямой  и содержит точку
и содержит точку  вторая ограничена прямой
вторая ограничена прямой  и содержит точку
и содержит точку 
 зная координаты точек
зная координаты точек  и
и 
 или
или 
 получим
получим  Следует, первая полуплоскость обозначается неравенством
Следует, первая полуплоскость обозначается неравенством
 и содержит точку
и содержит точку  обозначается неравенством:
обозначается неравенством:
 и содержит точку
и содержит точку  обозначается неравенством:
обозначается неравенством:
 обозначается системой неравенств
обозначается системой неравенств
 или
или  ) рассматривать не строгие неравенства (
) рассматривать не строгие неравенства (  или
или  ), то обозначенная ими область включается и границы этих полуплоскостей.
), то обозначенная ими область включается и границы этих полуплоскостей.
 включая ее как внутренние, так и граничные точки, то есть и точки отрезков
включая ее как внутренние, так и граничные точки, то есть и точки отрезков 










